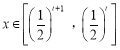Question

【题目】已知函数f（x）=lnx，g（x）=f（x）+ax2+bx，其中函数g（x）的图象在点（1，g（1））处的切线平行于x轴．
（1）确定a与b的关系；
（2）若a≥0，试讨论函数g（x）的单调性．

Answer 1

【答案】
（1）解：依题意得g（x）=lnx+ax2+bx，

则

由函数g（x）的图象在点（1，g（1））处的切线平行于x轴得：g'（1）=1+2a+b=0，

∴b=﹣2a﹣1

（2）解：由（1）得 ．

∵函数g（x）的定义域为（0，+∞），

∴当a=0时， ．

由g'（x）＞0，得0＜x＜1，由g'（x）＜0，得x＞1，

当a＞0时，令g'（x）=0，得x=1或 ，

若 ，即 ，

由g'（x）＞0，得x＞1或 ，

由g'（x）＜0，得 ；

若 ，即 ，

由g'（x）＞0，得 或0＜x＜1，

由g'（x）＜0，得

若 ，即 ，在（0，+∞）上恒有g'（x）≥0

综上可得：当a=0时，函数g（x）在（0，1）上单调递增，在（1，+∞）上单调递减；

当 时，函数g（x）在（0，1）上单调递增，

在 上单调递减，在 上单调递增；

当 时，函数g（x）在（0，+∞）上单调递增；

当 时，函数g（x）在 上单调递增，

在 上单调递减，在（1，+∞）上单调递增

【解析】（1）求出函数的导数，利用切线与x轴平行，推出结果．（2）求出函数的导数与函数g（x）的定义域，通过当a=0时，当a＞0时，分别求解函数的极值点，判断函数的单调性，即可得到结论．