题目内容
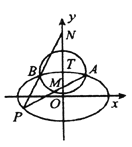
【题目】已知圆![]() 与圆
与圆![]()
(1)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两个不同点,求
两个不同点,求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 有无数对互相垂直的直线
有无数对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() 满足题意
满足题意
【解析】试题分析:(1)动直线恒过定点![]() ,根据圆的几何条件可得
,根据圆的几何条件可得![]() 取最小值时,
取最小值时, ![]() ,根据垂径定理解出
,根据垂径定理解出![]() 的最小值;(2)两弦长相等转化为对应圆心距相等,根据点到直线距离公式展开得关于斜率k的恒等式,再根据恒等式成立的条件解出点
的最小值;(2)两弦长相等转化为对应圆心距相等,根据点到直线距离公式展开得关于斜率k的恒等式,再根据恒等式成立的条件解出点![]() 坐标
坐标
试题解析:(1)直线![]() 过定点
过定点![]() ,
, ![]() 取最小值时,
取最小值时, ![]()
![]() ,∴
,∴![]()
(2)设![]() ,斜率不存在时不符合题意,舍去;斜率存在时,则
,斜率不存在时不符合题意,舍去;斜率存在时,则![]() 即
即![]() ,
, ![]() 即
即![]() ,
, ![]()
由题意可知,两弦长相等也就是![]() 和
和![]() 相等即可,故
相等即可,故![]() ,∴
,∴![]() ,化简得:
,化简得: ![]() 对任意
对任意![]() 恒成立,故
恒成立,故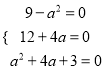 ,解得
,解得![]()
故存在点![]() 满足题意.
满足题意.

练习册系列答案
相关题目
【题目】某经销商从外地一水殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:
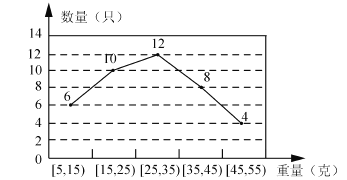
(1)记事件![]() 为:“从这批小龙虾中任取一只,重量不超过35
为:“从这批小龙虾中任取一只,重量不超过35![]() 的小龙虾”,求
的小龙虾”,求![]() 的估计值;
的估计值;
(2)试估计这批小龙虾的平均重量;
(3)为适应市场需求,制定促销策略.该经销商又将这批小龙虾分成三个等级,并制定出销售单价,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量( |
|
|
|
单价(元/只) | 1.2 | 1.5 | 1.8 |
试估算该经销商以每千克至多花多少元(取整数)收购这批小龙虾,才能获得利润?