题目内容
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当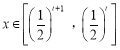 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在非负实数![]() 、
、![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
【答案】⑴![]() ;⑵
;⑵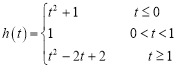 ;⑶存在
;⑶存在![]() 满足题意.
满足题意.
【解析】
试题分析:对问题⑴,根据题目条件首先要对实数![]() 的取值进行分类讨论,再结合极端不等式恒成立即可求出函数
的取值进行分类讨论,再结合极端不等式恒成立即可求出函数![]() 的定义域为
的定义域为![]() 时实数
时实数![]() 的取值范围;对于问题⑵,根据二次函数的单调性并结合对参数
的取值范围;对于问题⑵,根据二次函数的单调性并结合对参数![]() 的分类讨论,即可求得函数
的分类讨论,即可求得函数![]() 的最小值
的最小值![]() ;对问题⑶,根据二次函数的单调性以及函数与方程的思想即可知道存在符合题意的实数
;对问题⑶,根据二次函数的单调性以及函数与方程的思想即可知道存在符合题意的实数![]() 、
、![]() 的值.
的值.
试题解析:⑴![]() 定义域为
定义域为![]() .
.
所以![]() 对一切
对一切![]() 成立. ……………………1分
成立. ……………………1分
当![]() 时,
时,![]() 不可能对一切
不可能对一切![]() 成立. ……………………2分
成立. ……………………2分
所以![]() ,即
,即![]() 解得
解得![]() .
.
综上![]() . ……………………4分
. ……………………4分
⑵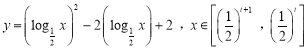 ,
,
令![]() ,
,
所以![]() ……………………5分
……………………5分
当![]() 时,
时,![]() . ……………………6分
. ……………………6分
当![]() 时,
时,![]() . ……………………7分
. ……………………7分
当![]() 时,
时,![]() . ……………………8分
. ……………………8分
所以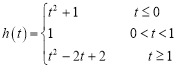 ……………………9分
……………………9分
⑶![]() 在
在![]() 上是增函数,
上是增函数,
若存在非负实数![]() 、
、![]() 满足题意,则
满足题意,则![]() ,………………………………10分
,………………………………10分
即![]() 、
、![]() 是方程
是方程![]() 的两非负实根,且
的两非负实根,且![]() ,
,
所以![]() .
.
即存在![]() 满足题意………………………………12分.
满足题意………………………………12分.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
