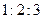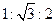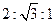题目内容
在△ABC中,已知角A、B、C对应的边分别为a、b、c,.且 C=2A.cos A=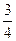
(1)求cosC和cosB的值;
(2)当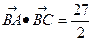 时,求a、b、c的值.
时,求a、b、c的值.
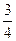
(1)求cosC和cosB的值;
(2)当
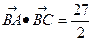 时,求a、b、c的值.
时,求a、b、c的值.⑴cosC=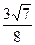 , cosB =
, cosB =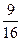 ⑵a=4,b=5,c=6
⑵a=4,b=5,c=6
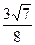 , cosB =
, cosB =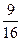 ⑵a=4,b=5,c=6
⑵a=4,b=5,c=6(1)cosC=cos2A=2cos2A-1=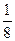 ; sinA=
; sinA=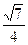 , cosC=
, cosC=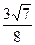 。
。
∴cosB=-cos(A+C)=sinAsinC-cosAcosC=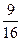 。
。
(2)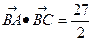
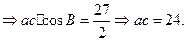
由正弦定理得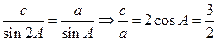 .
.
解得a=4,c=6.
再由余弦定理知b2=a2+c2-2ac·cosB= 42+62-48×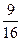 =25,b=5.
=25,b=5.
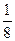 ; sinA=
; sinA=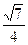 , cosC=
, cosC=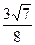 。
。∴cosB=-cos(A+C)=sinAsinC-cosAcosC=
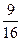 。
。(2)
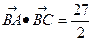
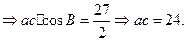
由正弦定理得
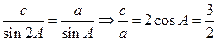 .
.解得a=4,c=6.
再由余弦定理知b2=a2+c2-2ac·cosB= 42+62-48×
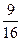 =25,b=5.
=25,b=5.
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 中,角
中,角 、
、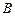 、
、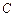 的对边分别为
的对边分别为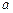 、
、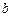 、
、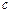 ,若
,若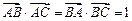 .
.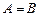 ;⑵求边长
;⑵求边长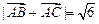 ,求△
,求△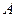 处的雷达观测站发现其北偏东
处的雷达观测站发现其北偏东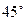 ,相距
,相距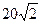 海里的
海里的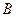 处有一货船正以匀速直线行驶,
处有一货船正以匀速直线行驶,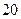 分钟后又测得该船只位于点
分钟后又测得该船只位于点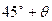 (其中
(其中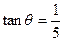 ,
,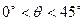 )且与点
)且与点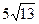 海里的位置
海里的位置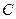 .(Ⅰ)求该船的行驶速度;(Ⅱ)在点
.(Ⅰ)求该船的行驶速度;(Ⅱ)在点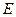 处有一暗礁(不考虑暗礁的面积),如果货船继续前行,它是否有触礁的危险?说明理由
处有一暗礁(不考虑暗礁的面积),如果货船继续前行,它是否有触礁的危险?说明理由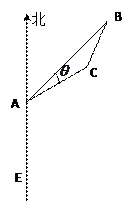

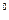 .则a= 。
.则a= 。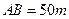 ,
,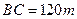 ,于A处测得水深
,于A处测得水深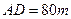 ,于B处测得水深
,于B处测得水深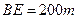 ,于C处测得水深
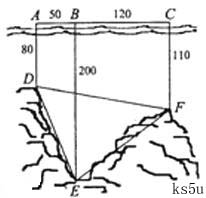
,于C处测得水深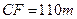 ,求∠DEF的余弦值。
,求∠DEF的余弦值。 

 、
、 、
、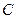 为
为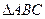 的三个内角,且其对边分别为
的三个内角,且其对边分别为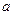 、
、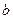 、
、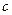 ,若
,若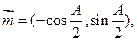
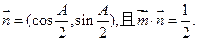
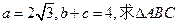 的面积.
的面积.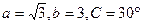 ,则A= 。
,则A= 。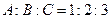 ,则
,则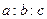 等于( )
等于( )