题目内容
6.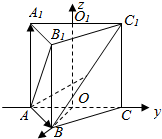 如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.
如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.(1)求正三棱柱ABC-A1B1C1的体积.
(2)若M为BC1的中点,求异面直线AM与BO所成角的余弦.
分析 (1)取A1B1的中点D,连接BD,则C1D⊥AB1,证明△AA1B1∽△DB1B,求出A1B1=2,即可求出正三棱柱ABC-A1B1C1的体积;
(2)利用向量的夹角公式,即可求异面直线AM与BO所成角的余弦.
解答  解:(1)取A1B1的中点D,连接BD,则C1D⊥AB1,
解:(1)取A1B1的中点D,连接BD,则C1D⊥AB1,
∵AB1⊥BC1,BC1∩C1D=C1,
∴AB1⊥平面BC1D,
∴AB1⊥BD,
∴△AA1B1∽△DB1B,
∵AA1=$\sqrt{2}$,
∴$\frac{\sqrt{2}}{D{B}_{1}}$=$\frac{{A}_{1}{B}_{1}}{\sqrt{2}}$,
∴A1B1=2,
∴正三棱柱ABC-A1B1C1的体积V=$\frac{\sqrt{3}}{4}×4×\sqrt{2}$=$\sqrt{6}$.
(2)由题意,A(0,-1,0),B($\sqrt{3}$,0,0),O(0,0,0),M($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),
∴$\overrightarrow{AM}$=($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$,$\frac{\sqrt{2}}{2}$),$\overrightarrow{OB}$=($\sqrt{3}$,0,0),
∴异面直线AM与BO所成角的余弦=$\frac{\frac{3}{2}}{\frac{\sqrt{15}}{2}•\sqrt{3}}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查线面垂直,考查正三棱柱ABC-A1B1C1的体积、求异面直线AM与BO所成角的余弦,考查向量方法的运用,属于中档题.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
16.已知$\overrightarrow{a}$,$\overrightarrow{b}$是平面内互不相等的两个非零向量,且|$\overrightarrow{a}$|=1,$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°,则|$\overrightarrow{b}$|的取值范围是( )
| A. | (0,$\sqrt{3}$] | B. | [1,$\sqrt{3}$] | C. | (0,2] | D. | [$\sqrt{3}$,2] |