题目内容
15.若椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与x轴、y轴正半轴分别交于点A、B,点C是椭圆上位于第一象限的点,则四边形OACB面积的最大值为$\frac{15\sqrt{2}}{2}$.分析 求得A,B的坐标,设C(5cosα,3sinα)(0<α<$\frac{π}{2}$),由四边形OACB面积为S=S△OBC+S△OAC═$\frac{15}{2}$(cosα+sinα),由两角和的正弦公式和正弦函数的最值,可得最大值.
解答 解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,可得a=5,b=3,
可设C(5cosα,3sinα)(0<α<$\frac{π}{2}$),
即有A(5,0),B(0,3),
四边形OACB面积为S=S△OBC+S△OAC
=$\frac{1}{2}$•3•5cosα+$\frac{1}{2}$•5•3sinα
=$\frac{15}{2}$(cosα+sinα)=$\frac{15\sqrt{2}}{2}$sin(α+$\frac{π}{4}$),
当α=$\frac{π}{4}$时取得最大值,且为$\frac{15\sqrt{2}}{2}$.
故答案为:$\frac{15\sqrt{2}}{2}$.
点评 本题考查椭圆的参数方程的运用,考查三角函数的最值的求法,注意运用正弦函数的最值,属于中档题.

练习册系列答案
相关题目
5.在一定范围内,对7块土质相同、形状大小也相同的试验田进行化肥用量对水稻产量影响的试验,得到的对应数据如表(单位:kg):
根据表可得回归方程$\widehat{y}$=bx+$\widehat{a}$中的b为4.8,据此估计,当化肥用量为55kg时,水稻产量为519.3kg.
| 施化肥量x | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 水稻产量y | 330 | 345 | 365 | 405 | 445 | 450 | 455 |
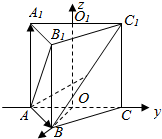 如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.
如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.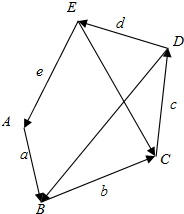 向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题:
向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{e}$如图所示,解答下列各题: