题目内容
17.直线y=x+b是椭圆$\frac{{x}^{2}}{1{2}^{2}}$+$\frac{{y}^{2}}{{5}^{2}}$=1的切线,求b的值.分析 联立直线方程与椭圆方程,化为关于x的一元二次方程后利用判别式等于0求得b值.
解答 解:联立$\left\{\begin{array}{l}{y=x+b}\\{\frac{{x}^{2}}{1{2}^{2}}+\frac{{y}^{2}}{{5}^{2}}=1}\end{array}\right.$,可得169x2+288bx+144b2-3600=0,
由△=(288b)2-4×169(144b2-360)=0,得
-14400b2+243360=0,即1440b2=24336,
∴b=$±\frac{13\sqrt{10}}{10}$.
点评 本题考查椭圆的简单性质,考查利用判别式法判断方程根的问题,是基础的计算题.

练习册系列答案
相关题目
7.已知命题p、q,则“p∧q是真命题”是“¬p为假命题”的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
5.在一定范围内,对7块土质相同、形状大小也相同的试验田进行化肥用量对水稻产量影响的试验,得到的对应数据如表(单位:kg):
根据表可得回归方程$\widehat{y}$=bx+$\widehat{a}$中的b为4.8,据此估计,当化肥用量为55kg时,水稻产量为519.3kg.
| 施化肥量x | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 水稻产量y | 330 | 345 | 365 | 405 | 445 | 450 | 455 |
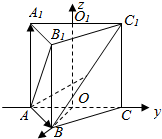 如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.
如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.