题目内容
16.已知$\overrightarrow{a}$,$\overrightarrow{b}$是平面内互不相等的两个非零向量,且|$\overrightarrow{a}$|=1,$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°,则|$\overrightarrow{b}$|的取值范围是( )| A. | (0,$\sqrt{3}$] | B. | [1,$\sqrt{3}$] | C. | (0,2] | D. | [$\sqrt{3}$,2] |
分析 如图所示,设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}$=$\overrightarrow{a}-\overrightarrow{b}$.由于|$\overrightarrow{a}$|=1,$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°,可得△OAB中,OA=1,∠OBA=30°.由正弦定理可得:△OAB的外接圆的半径r=1.则点B为圆上的动点.由图可令$\overrightarrow{b}=\overrightarrow{OB}$=(1+cosθ,sinθ),则|$\overrightarrow{b}$|的取值范围可求.
解答 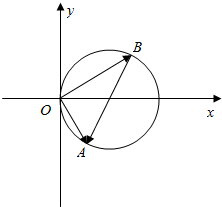 解:如图所示,设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}$=$\overrightarrow{a}-\overrightarrow{b}$.
解:如图所示,设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}$=$\overrightarrow{a}-\overrightarrow{b}$.
由于|$\overrightarrow{a}$|=1,$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为150°,可得△OAB中,OA=1,∠OBA=30°.
由正弦定理可得:△OAB的外接圆的半径r=1.则点B为圆上的动点.
由图可令$\overrightarrow{b}=\overrightarrow{OB}$=(1+cosθ,sinθ),
则$|\overrightarrow{b}|=\sqrt{(1+cosθ)^{2}+si{n}^{2}θ}$=$\sqrt{2+2cosθ}$.
∴$|\overrightarrow{b}|∈(0,2]$.
故选:C.
点评 本题考查了数量积运算性质、三角函数的单调性、正弦定理、三角形外接圆的性质,考查了数形结合的能力、推理能力与计算能力,属于有一定难题题目.

| A. | 第一象限 | B. | 第一、二象限 | C. | 第一、三象限 | D. | 第二、四象限 |
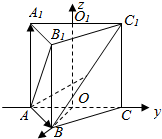 如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.
如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.