题目内容
已知顶点在原点,焦点在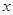 轴上的抛物线被直线
轴上的抛物线被直线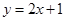 截得的弦长为
截得的弦长为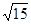 ,(1)求抛物线的方程;(2)若抛物线与直线
,(1)求抛物线的方程;(2)若抛物线与直线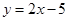 无公共点,试在抛物线上求一点,使这点到直线
无公共点,试在抛物线上求一点,使这点到直线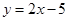 的距离最短。
的距离最短。
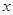 轴上的抛物线被直线
轴上的抛物线被直线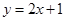 截得的弦长为
截得的弦长为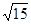 ,(1)求抛物线的方程;(2)若抛物线与直线
,(1)求抛物线的方程;(2)若抛物线与直线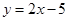 无公共点,试在抛物线上求一点,使这点到直线
无公共点,试在抛物线上求一点,使这点到直线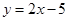 的距离最短。
的距离最短。(1)设抛物线的方程为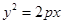 ,则
,则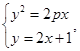 消去
消去 得
得
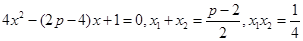 ……………2
……………2
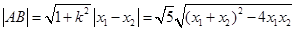
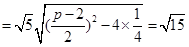 ,………4
,………4
则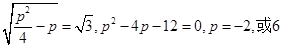
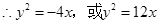 …………6
…………6
(2)解法一、显然抛物线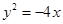 与直线
与直线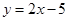 无公共点,设点
无公共点,设点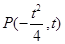 为抛物线
为抛物线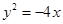 上的任意一点,点P到直线
上的任意一点,点P到直线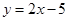 的距离为
的距离为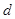 ,则 ……………7
,则 ……………7
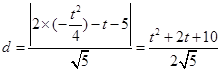 ……………10
……………10
当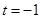 时,
时,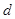 取得最小值,此时
取得最小值,此时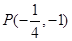 为所求的点 ……………12
为所求的点 ……………12
解法二、显然抛物线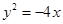 与直线
与直线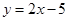 无公共点,设与直线
无公共点,设与直线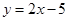 平行且与抛物线
平行且与抛物线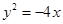 相切的直线方程为
相切的直线方程为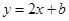 ,切点为P,则点P即为所求点。……7
,切点为P,则点P即为所求点。……7
由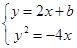 消去
消去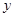 并化简得:
并化简得: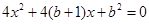 , ……………9
, ……………9
∵直线与抛物线相切,∴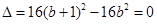 ,解得:
,解得: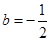
把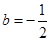 代入方程
代入方程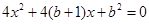 并解得:
并解得: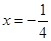 ,∴
,∴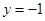
故所求点为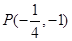 。
。
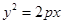 ,则
,则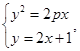 消去
消去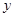 得
得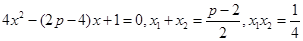 ……………2
……………2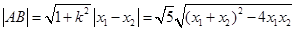
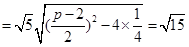 ,………4
,………4则
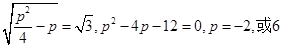
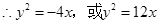 …………6
…………6(2)解法一、显然抛物线
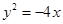 与直线
与直线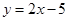 无公共点,设点
无公共点,设点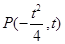 为抛物线
为抛物线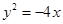 上的任意一点,点P到直线
上的任意一点,点P到直线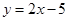 的距离为
的距离为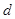 ,则 ……………7
,则 ……………7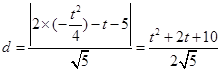 ……………10
……………10当
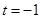 时,
时,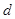 取得最小值,此时
取得最小值,此时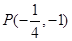 为所求的点 ……………12
为所求的点 ……………12解法二、显然抛物线
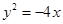 与直线
与直线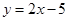 无公共点,设与直线
无公共点,设与直线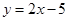 平行且与抛物线
平行且与抛物线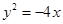 相切的直线方程为
相切的直线方程为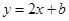 ,切点为P,则点P即为所求点。……7
,切点为P,则点P即为所求点。……7由
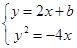 消去
消去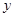 并化简得:
并化简得: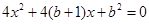 , ……………9
, ……………9∵直线与抛物线相切,∴
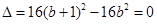 ,解得:
,解得: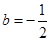
把
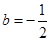 代入方程
代入方程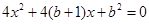 并解得:
并解得: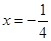 ,∴
,∴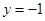
故所求点为
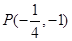 。
。略

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
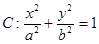 经过点(0,
经过点(0,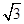 ),离心率为
),离心率为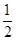 ,直线l经过椭圆C的右焦点F交
,直线l经过椭圆C的右焦点F交 椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.
椭圆于A、B两点,点A、F、B在直线x=4上的射影依次为点D、K、E.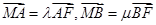 ,当直线l的倾斜角变化时,探求
,当直线l的倾斜角变化时,探求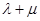 的值是否为定值?若是,求出
的值是否为定值?若是,求出
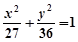 的焦点相同,且它们一个交点的纵坐标为4,则双曲线的虚轴长为
的焦点相同,且它们一个交点的纵坐标为4,则双曲线的虚轴长为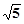
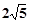
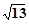
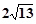
 ,使得点
,使得点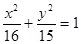
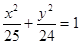
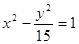
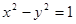
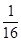 ,0)
,0)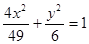 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且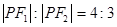 ,则
,则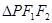 的面积为( )
的面积为( )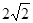
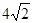
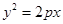 的准线与双曲线
的准线与双曲线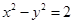 的左准线重合,则p的值为 ▲
的左准线重合,则p的值为 ▲ 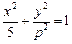 的左焦点在抛物线
的左焦点在抛物线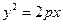 的准线上,则p的值为_______;
的准线上,则p的值为_______;