题目内容
(本小题満分12分)
已知一条曲线上的每个点M到A(1,0)的距离减去它到y轴的距离差都是1.
(1)求曲线的方程;
(2)讨论直线y=kx+1(k∈R)与曲线的公共点个数
已知一条曲线上的每个点M到A(1,0)的距离减去它到y轴的距离差都是1.
(1)求曲线的方程;
(2)讨论直线y=kx+1(k∈R)与曲线的公共点个数
解:(1)设点M(x,y)是曲线上任意一点,则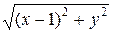 -|x|=1,
-|x|=1,
化简得:y2=2x+2|x|
所求曲线的方程.C1:当x³0时, y2=4x;C2:当x<0时,y=0.
(2)直线y=kx+1过定点(0,1),
y=kx+1,与y2=4x联列:ky2- 4y+4="0," D=16-16k
4y+4="0," D=16-16k
 当k=0时,直线与C1有一个公共点,而与C2没有公共点,共1个公共点;
当k=0时,直线与C1有一个公共点,而与C2没有公共点,共1个公共点;
当k=1时, D=0,直线与C1和C2各一个公共点,共2个公共点;
 当0
当0 <k<1时,D>0,直线与C1有2个公共点,和C2一个交点,共3个公共点;
<k<1时,D>0,直线与C1有2个公共点,和C2一个交点,共3个公共点;
当k<0时,D>0,直线与C 1有两个公共点,和C2没有公共点,共2个公共点;
1有两个公共点,和C2没有公共点,共2个公共点;
当k>1时, D<0,直线与C1没有公共点,和C2有1个公共点,共1个公共点;
所以:当k=0,或k>1时,直线与曲线有1个公共点;
当k=1,或k<0时,直线与曲线有2个公共点;
当0<k<1时,直线与曲线有3个公共点.
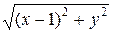 -|x|=1,
-|x|=1,化简得:y2=2x+2|x|
所求曲线的方程.C1:当x³0时, y2=4x;C2:当x<0时,y=0.
(2)直线y=kx+1过定点(0,1),
y=kx+1,与y2=4x联列:ky2-
 4y+4="0," D=16-16k
4y+4="0," D=16-16k 当k=0时,直线与C1有一个公共点,而与C2没有公共点,共1个公共点;
当k=0时,直线与C1有一个公共点,而与C2没有公共点,共1个公共点;当k=1时, D=0,直线与C1和C2各一个公共点,共2个公共点;
 当0
当0 <k<1时,D>0,直线与C1有2个公共点,和C2一个交点,共3个公共点;
<k<1时,D>0,直线与C1有2个公共点,和C2一个交点,共3个公共点;当k<0时,D>0,直线与C
 1有两个公共点,和C2没有公共点,共2个公共点;
1有两个公共点,和C2没有公共点,共2个公共点;当k>1时, D<0,直线与C1没有公共点,和C2有1个公共点,共1个公共点;
所以:当k=0,或k>1时,直线与曲线有1个公共点;
当k=1,或k<0时,直线与曲线有2个公共点;
当0<k<1时,直线与曲线有3个公共点.
略

练习册系列答案
相关题目
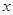 轴上的抛物线被直线
轴上的抛物线被直线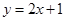 截得的弦长为
截得的弦长为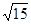 ,(1)求抛物线的方程;(2)若抛物线与直线
,(1)求抛物线的方程;(2)若抛物线与直线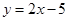 无公共点,试在抛物线上求一点,使这点到直线
无公共点,试在抛物线上求一点,使这点到直线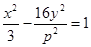 的左焦点在抛物线
的左焦点在抛物线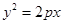 的准线上,则
的准线上,则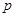 的值为 ( )
的值为 ( ) 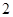
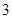
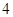
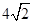
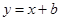 与曲线
与曲线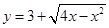 有公共点,则实数
有公共点,则实数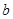 的取值范围是( ▲ )
的取值范围是( ▲ ) 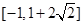
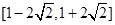
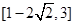
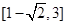
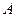 (1,0)和定圆B:
(1,0)和定圆B: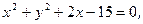 动圆P和定圆B相切并过A点,
动圆P和定圆B相切并过A点,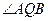 的最大值。
的最大值。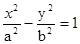 与椭圆
与椭圆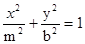 (a>0,m>b>0)的离心率互为倒数,那
(a>0,m>b>0)的离心率互为倒数,那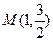 ,两个焦点为
,两个焦点为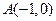 ,
,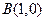 ,O为坐标原点。
,O为坐标原点。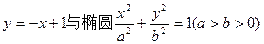 相交于A、B两点。
相交于A、B两点。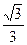 ,焦距为2,求椭圆的标准方程;
,焦距为2,求椭圆的标准方程;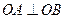 (其中O为坐标原点),当椭圆的离率
(其中O为坐标原点),当椭圆的离率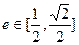 时,求椭圆的长轴长的最大值。
时,求椭圆的长轴长的最大值。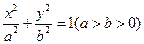 的一个焦点,若椭圆上存在点A使
的一个焦点,若椭圆上存在点A使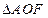 为正三角形,那么椭圆的离心率为
为正三角形,那么椭圆的离心率为