题目内容
1.F1、F2为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的焦点,A、B分别为双曲线的左、右顶点,以F1F2为直径的圆与双曲线的渐近线于B,C两点,若△ABC的面积为$\frac{1}{2}$c2,则该双曲线的离心率为$\sqrt{2}$.分析 利用△ABC的面积为$\frac{1}{2}$c2,求出双曲线的渐近线的倾斜角,即可求出该双曲线的离心率.
解答 解:设双曲线的渐近线的倾斜角为α(0<α<$\frac{π}{2}$),
由题意,△ABC的面积为$\frac{1}{2}$c2,则$\frac{1}{2}$c2sin2α=$\frac{1}{2}$c2,
∴α=45°,
∴b=a,
∴c=$\sqrt{2}$a,
∴e=$\frac{c}{a}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查双曲线的离心率,考查三角形面积的计算,求出b=a是关键.

练习册系列答案
相关题目
12.已知集合A={x|-1≤x≤1},B={x|x>0},则A∩(∁RB)=( )
| A. | {x|-1≤x≤0} | B. | {x|-1≤x<0} | C. | {x|-1≤x≤1} | D. | {x|x≤1} |
 已知菱形ABCD中,∠DAB=60°,点G是正△PAD的边AD的中
已知菱形ABCD中,∠DAB=60°,点G是正△PAD的边AD的中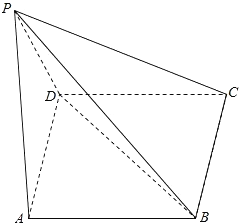 如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.
如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.