题目内容
6.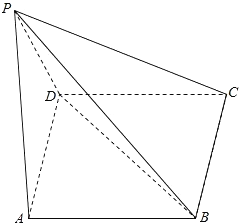 如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.
如图,四凌锥P-ABCD而底面ABCD是矩形,侧面PAD是等腰直角三角形∠APD=90°,且平面PAD⊥平面ABCD.(Ⅰ)求证:平面PAD⊥平面PCD;
(Ⅱ)在AD=2,AB=4,求三棱锥P-ABD的体积;
(Ⅲ)在条件(Ⅱ)下,求四棱锥P-ABCD外接球的表面积.
分析 (I)由底面ABCD为矩形可得CD⊥AD,由平面PAD⊥平面ABCD,从而CD⊥平面PAD,得到结论;
(II)由(I)证明可知PA为三棱锥P-ABD的高,底面是直角三角形,代入公式计算即可得到棱锥体积;
(III)取BD中点M,过M作MN⊥平面ABCD,则球心O在直线MN上,连由OP=OA可知OM=$\frac{1}{2}$PA=1,于是球的半径OA=$\sqrt{A{M}^{2}+O{M}^{2}}$,从而求出球的表面积.
解答  解:(I)∵四边形ABCD是矩形,∴AD⊥CD,
解:(I)∵四边形ABCD是矩形,∴AD⊥CD,
又∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD?平面ABCD,
∴CD⊥平面PAD,∵CD?平面PCD,
∴平面PAD⊥平面PCD.
(II)过P作PE⊥AD,垂足为E,∵△PAD是等腰直角三角形,∠APD=90°,
∴PE=$\frac{1}{2}AD$=1.
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PE?平面PAD,PE⊥AD,
∴PE⊥平面ABCD,
∴V棱锥P-ABD=$\frac{1}{3}$S△ABD•PE=$\frac{1}{3}$•$\frac{1}{2}$•2•4•1=$\frac{4}{3}$.
(III)取BD中点M,过M作MN⊥平面ABCD,则球心O在直线MN上,
连接AM,则AM=$\frac{1}{2}$$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{5}$.
∵PE⊥平面ABCD,∴MN∥PE.
∵四棱锥P-ABCD内接于球,
∴OP=OA,
∴OM=$\frac{1}{2}$PE=$\frac{1}{2}$,
∴OA=$\sqrt{O{M}^{2}+A{M}^{2}}$=$\frac{\sqrt{21}}{2}$.
∴S⊙O=4πOA2=21π.
点评 本题考查了面面垂直的判定,几何体体积和圆内接几何体的特征,正确找到圆心位置是关键.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | -4 | B. | 2 | C. | 8 | D. | $-\frac{10}{3}$ |

 如图,已知一个圆锥的底面半径为R,高为H.一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.求:
如图,已知一个圆锥的底面半径为R,高为H.一个圆柱的下底面在圆锥的底面上,且圆柱的上底面为圆锥的截面,设圆柱的高为x.求: