题目内容
16．已知圆锥的底面半径为1，且它的侧面展开图是一个半圆，则这个圆锥的体积为$\frac{\sqrt{3}π}{3}$．分析 利用圆锥的底面周长等于侧面展开图的扇形弧长，求出圆锥的母线长，进而可得高，即可求出圆锥的体积．
解答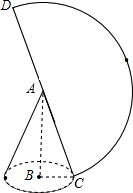 
解：∵圆锥的侧面展开图是一个半圆，圆锥的底面周长为：2π，即侧面展开图半圆的弧长是2π，半圆的半径就是圆锥的母线：2，
圆锥的高为：$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∴圆锥的体积=$\frac{1}{3}π•{1}^{2}•\sqrt{3}$=$\frac{\sqrt{3}π}{3}$．
故答案为：$\frac{\sqrt{3}π}{3}$．
点评 本题综合考查有关扇形和圆锥的相关计算．解题思路：解决此类问题时要紧紧抓住两者之间的两个对应关系：（1）圆锥的母线长等于侧面展开图的扇形半径；（2）圆锥的底面周长等于侧面展开图的扇形弧长，正确对这两个关系的记忆是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
6．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的左、右焦点分别为F1，F2，过F2的直线与双曲线C的右支相交于P，Q两点，若PQ⊥PF1，且|PF1|=|PQ|，则双曲线的离心率e=（ ）
| A． | $\sqrt{2}$+1 | B． | 2$\sqrt{2}$+1 | C． | $\sqrt{5+2\sqrt{2}}$ | D． | $\sqrt{5-2\sqrt{2}}$ |
7．已知A，B，C，D是球面上的四个点，其中A，B，C在同一圆周上，若D不在A，B，C所在的圆周上，则从这四点中的任意两点的连线中取2条，这两条直线是异面直线的概率等于（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
在正三棱柱ABC-A1B1C1中，E是AB的中点，D是CC1上一点．