题目内容
13.若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点坐标为(a-$\frac{b}{2}$,0),则椭圆的离心率e=$\frac{3}{5}$.分析 设椭圆的右焦点为(c,0),由题意可得c=a-$\frac{b}{2}$,又a2-b2=c2,消去b,解方程即可得到离心率.
解答 解:设椭圆的右焦点为(c,0),由题意可得
c=a-$\frac{b}{2}$,又a2-b2=c2,
即有a2-c2=4(a-c)2,
即为5c2+3a2-8ac=0,
由e=$\frac{c}{a}$,可得5e2-8e+3=0,
解得e=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查椭圆的方程和性质,主要考查离心率的求法,注意运用解含有e的方程,考查运算能力,属于基础题.

练习册系列答案
相关题目

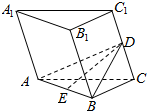 在正三棱柱ABC-A1B1C1中,E是AB的中点,D是CC1上一点.
在正三棱柱ABC-A1B1C1中,E是AB的中点,D是CC1上一点.