题目内容
4.已知向量$\overrightarrow{a}$=(-3,4),$\overrightarrow{b}$=(1,m),若$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,则m=7.分析 根据向量的坐标公式,以及向量垂直的定义直接计算即可.
解答 解:由题可知:$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=(-3,4)•[(-3,4)-(1,m)]
=(-3,4)•(-4,4-m)
=12+16-4m=0,
即m=7,
故答案为:7.
点评 本题考查平面向量数量积的运算,注意解题方法的积累,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.不等式$\frac{x-1}{{x}^{2}-4}$>0的解集是( )
| A. | (-2,1)∪(2,+∞) | B. | (2,+∞) | C. | (-2,1) | D. | (-∞,-2)∪(1,+∞) |
15.等比数列的首项是-5,公比是-2,则它的第6项是( )
| A. | -160 | B. | 160 | C. | 90 | D. | 10 |
16.若框图所给的程序运行结果为S=90.那么判断框中应填入后的条件是( )
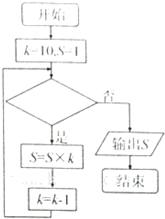

| A. | k=9 | B. | k≤8 | C. | k<8 | D. | k>8 |
13.已知复数z=1-i(i为虚数单位),$\overline{z}$是z的共轭复数,则|$\frac{1}{z}$|的值为( )
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
14.甲、乙两位同学各拿出六张游戏牌,用作投骰子的奖品,两人商定:骰子朝上的面的点数为奇数时甲得1分,否则乙得1分,先积得3分者获胜得所有12张游戏牌,并结束游戏.比赛开始后,甲积2分,乙积1分,这时因意外事件中断游戏,以后他们不想再继续这场游戏,下面对这12张游戏牌的分配合理的是( )
| A. | 甲得9张,乙得3张 | B. | 甲得6张,乙得6张 | ||
| C. | 甲得8张,乙得4张 | D. | 甲得10张,乙得2张 |
 如图是三棱柱被平面截去一部分后剩余的几何体的三视图,则截掉的几何体与三视图所示的几何体的体积之比为1:2.
如图是三棱柱被平面截去一部分后剩余的几何体的三视图,则截掉的几何体与三视图所示的几何体的体积之比为1:2.