题目内容
2.不等式$\frac{x-1}{{x}^{2}-4}$>0的解集是( )| A. | (-2,1)∪(2,+∞) | B. | (2,+∞) | C. | (-2,1) | D. | (-∞,-2)∪(1,+∞) |
分析 根据不等式的解法解得即可.
解答  解:不等式$\frac{x-1}{{x}^{2}-4}$>0等价于(x+2)(x-1)(x-2)>0,
解:不等式$\frac{x-1}{{x}^{2}-4}$>0等价于(x+2)(x-1)(x-2)>0,
令(x+2)(x-1)(x-2)=0,
解得x=-2,或x=1,或x=2,
如图所示,
由图象可知不等式的解集为(-2,1)∪(2,+∞),
故选:A.
点评 本题利用穿根法解高次不等式,第一步:通过不等式的诸多性质对不等式进行移项,使得右侧为0.(注意:一定要保证x前的系数为正数)
第二步:将不等号换成等号解出所有根,
第三步:在数轴上从左到右依次标出各根,
第四步:画穿根线:以数轴为标准,从“最右根”的右上方穿过根,往左下画线,然后又穿过“次右根”上去,一上一下依次穿过各根.
第五步:观察不等号,如果不等号为“>”,则取数轴上方,穿根线以内的范围;如果不等号为“<”则取数轴下方,穿根线以内的范围.x的次数若为偶数则不穿过,即奇过偶不过.

练习册系列答案
相关题目
13.下列程序的功能是( )
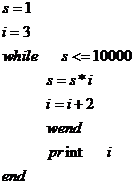
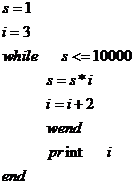
| A. | 求1×2×3×4×…×10 000的值 | |
| B. | 求2×4×6×8×…×10 000的值 | |
| C. | 求3×5×7×9×…×10 000的值 | |
| D. | 求满足1×3×5×…×n>10 000的最小正整数n |
10.平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$的面积是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
7.已知函数f(x)=loga(ax2-x)(a>0且a≠1).若f(x)在[2,4]上是增函数,则a的取值范围是( )
| A. | a<1 | B. | a>1 | C. | a<2 | D. | a>2 |
 如图,△ABC与△BCD都是边长为2的正三角形,AD=$\sqrt{6}$,PA⊥平面ABC
如图,△ABC与△BCD都是边长为2的正三角形,AD=$\sqrt{6}$,PA⊥平面ABC