题目内容

16．各项均为正数的等差数列{an}中，a4a9=36，则前12项和S12的最小值为（　　）
A．78B．48C．60D．72

分析 利用基本不等式，结合等差数列的求和及通项公式，即可求出前12项和S12的最小值．

解答 解：由题意，a4+a9≥2$\sqrt{{a}_{4}{a}_{9}}$=12，
∴S12=$\frac{12}{2}$（a1+a12）=6（a4+a9）≥72，
故选：D．

点评 本题考查基本不等式，考查等差数列的求和及通项公式，正确运用等差数列的求和及通项公式是关键．

练习册系列答案
相关题目
6．以直角坐标系的原点为极点，x轴正半轴为极轴，建立极坐标系，已知曲线c1的参数方程为$\left\{\begin{array}{l}{x=1+2cosα}\\{y=2+2sinα}\end{array}\right.$（α为参数），直线l的极坐标方程为θ=$\frac{π}{4}$．
（1）求曲线c1与直线l的直角坐标方程．
（2）若直线l与曲线c1交于两点A、B，求|AB|．
7．已知a，b，c分别为△ABC三个内角A，B，C的对边，bcosC+$\sqrt{3}$bsinC-a-c=0．
（Ⅰ）求∠B的值；
（Ⅱ）若b=$\sqrt{3}$，求a+c的最大值．
4．已知cosα=$\frac{4}{5}$，α∈（-$\frac{π}{2}$，0），则tan（$\frac{π}{4}$+$\frac{α}{2}$）的值是（　　）
A．2B．$\frac{2}{5}$C．-2D．-$\frac{1}{2}$
11．已知f（x）=sinxsin（x+$\frac{π}{6}$），$x∈[-\frac{π}{3}，\frac{π}{3}]$，则f（x）的最小值为$\frac{\sqrt{3}-2}{4}$．
1．数列{an}满足2an=an-1+an+1（n≥2），且a1+a3+a5=9，a3+a5+a7=15则a3+a4+a5=（　　）
A．9B．10C．11D．12
8．椭圆满足这样的光学性质：从椭圆的一个交点发射的光线，经椭圆反射后，反射光先经过椭圆的另一个交点，现设有一个水平放置的椭圆形台球盘，满足方程$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1，点A和B是它们的两个交点，当静止的小球放在点A处，从点A沿直线出发，经椭圆壁反弹后，再回到点A时，小球经过的路程是2或18或20．
5．一个算法的程序框图如图所示，若运行该程序后输出的结果为$\frac{4}{5}$，则判断框中应填入的条件是（　　）
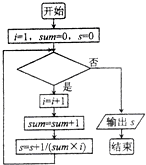
A．i≤5？B．i≤4？C．i≥4？D．i≥5？
6．设a＞0，b＞0，若$\sqrt{3}$是93a与3b的等比中项，则$\frac{2}{a}+\frac{1}{b}$的最小值为（　　）
A．1B．13+$4\sqrt{3}$C．2$\sqrt{3}$D．$\frac{13}{2}+2\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网