题目内容
【题目】如图，已知离心率为 
的椭圆C： 
+ 
=1（a＞b＞0）过点M（2，1），O为坐标原点，平行于OM的直线l交椭圆C于不同的两点A、B．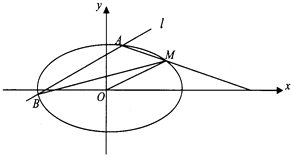 
（1）求椭圆C的方程．
（2）证明：直线MA、MB与x轴围成一个等腰三角形．
【答案】
（1）解：设椭圆C的方程为： 
+ 
=1（a＞b＞0），
由题意得：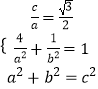 
，
解得a2=8，b2=2，
∴椭圆方程为 
．
（2）证明：由直线l∥OM，设l：y= 
，
将式子代入椭圆C得：x2+2mx+2m2﹣4=0，
设A（x1，y1），B（x2，y2），则x1+x2=﹣2m， 
，
设直线MA、MB的斜率分别为k1，k2，
则 
， 
，
∵k1+k2= 
=1+m 
=1+m 
=0，
故直线MA、MB与x轴围成一个等腰三角形．
【解析】（1）先由椭圆C： + =1（a＞b＞0）的离心率为 
和椭圆过点M（2，1），列出方程组，再由方程组求出a，b，由此能求出椭圆方程．（2）由直线l∥OM，设l：y= ，将式子代入椭圆C得：x2+2mx+2m2﹣4=0，设直线MA、MB的斜率分别为k1 ， k2 ， 欲证明直线MA、MB与x轴围成一个等腰三角形．只需证明：k1+k2=0即可．
【考点精析】掌握椭圆的标准方程是解答本题的根本，需要知道椭圆标准方程焦点在x轴：
，焦点在y轴：
．
练习册系列答案
相关题目
