题目内容
【题目】设f（x）是定义在[1，+∞）的函数，对任意正实数x，f（3x）=3f（x），且f（x）=1﹣|x﹣2|，1≤x≤3，则使得f（x）=f（2015）的最小实数x为（ ）
A.172
B.415
C.557
D.89
【答案】B
【解析】解：因为f（x）对于所有的正实数x均有f（3x）=3f（x），
所以f（x）=3f（ 
），
所以f（2015）=3f（ 
）=32f（ 
）=…=3nf（ 
），
当n=6时， 
∈（1，3），
所以f（2015）=36[1﹣ +2]=37﹣2015=172，
同理f（x）=3nf（ 
）= 
= 
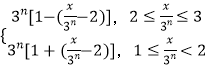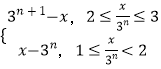，（n∈N*）
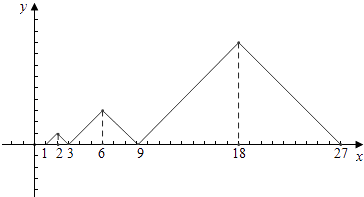
∵f（2）=1，∴f（6）=3f（2）=3，f（18）=3f（6）=32=9，
f（54）=3f（18）=33=27，f（162）=3f（54）=34=81，
f（486）=3f（162）=35=243，
即此时由f（x）=35f（ 
）=35（ ﹣1）=x﹣35=172
得x=35+172=243+172=415，
即使得f（x）=f（2015）的最小实数x为415，
所以答案是：B．
练习册系列答案
名校课堂系列答案
相关题目
