题目内容
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有 ![]() >0.
>0.
(Ⅰ)证明f(x)在[﹣1,1]上是增函数;
(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0
(Ⅲ)若f(x)≤t2﹣2at+1对x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.
【答案】解:(Ⅰ)任取﹣1≤x1<x2≤1,
则 ![]() ,
,
∵﹣1≤x1<x2≤1,∴x1+(﹣x2)≠0,
由已知 ![]() ,
,
∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),
∴f(x)在[﹣1,1]上是增函数;
(Ⅱ)∵f(x)是定义在[﹣1,1]上的奇函数,且在[﹣1,1]上是增函数,
∴不等式化为f(x2﹣1)<f(3x﹣3),
∴ 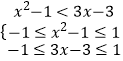 ,解得
,解得 ![]() ;
;
(Ⅲ)由(Ⅰ)知f(x)在[﹣1,1]上是增函数,
∴f(x)在[﹣1,1]上的最大值为f(1)=1,
要使f(x)≤t2﹣2at+1对x∈[﹣1,1]恒成立,只要t2﹣2at+1≥1t2﹣2at≥0,
设g(a)=t2﹣2at,对a∈[﹣1,1],g(a)≥0恒成立,
∴ ![]() ,
,
∴t≥2或t≤﹣2或t=0.
【解析】本题考查的是奇函数和增减性相结合的问题,用定义去证明函数的单调性。一元二次函数在指定区间内的最值问题,对称轴在指定区间内就能取到函数的最值,如果不在根据单调性去解决。

练习册系列答案
相关题目