题目内容
7.已知直线l1:2x+ay=3和l2:(a+2)x-y=1直线互相垂直,则实数a的值为( )| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
分析 两条直线A1x+B1y+C1=0与A2x+B2y+C2=0互相垂直的充要条件是:A1A2+B1B2=0,由此建立关于a的方程,解之即可得到实数a的值.
解答 解:∵直线l1:2x+ay=3和l2:(a+2)x-y=1直线互相垂直,
∴2(a+2)+(-1)×a=0,解之得a=-4,
故选:C.
点评 本题给出两条直线互相垂直,求参数a之值,着重考查了平面直角坐标系中两条直线互相垂直的充要条件的知识,属于基础题.

练习册系列答案
相关题目
15.已知抛物线y=$\frac{{x}^{2}}{4}$与直线y=$\frac{3}{4}$x+1交于点P,Q,则如图所示阴影部分的面积为( )
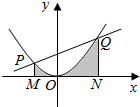

| A. | $\frac{65}{12}$ | B. | $\frac{85}{16}$ | C. | $\frac{143}{24}$ | D. | $\frac{95}{6}$ |
17.某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.
(1)求这些数据的线性回归方程;
(2)预测当广告费支出为9百万元时的销售额.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)求这些数据的线性回归方程;
(2)预测当广告费支出为9百万元时的销售额.
附:线性回归方程$\widehaty=\widehatbx+\widehata$中,$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.