题目内容
2.空间四边形ABCD中,对角线AC,BD与各边长均为1,O为△BCD的重心,M是AC的中点,E是AO的中点,求异面直线OM与BE所成的角为$\frac{π}{4}$.分析 连接BO并延长,交CD于F,以F为坐标原点建立空间坐标系,求出异面直线OM与BE的方向向量,代入向量夹角公式,可得答案.
解答 解:∵空间四边形ABCD中,各边长均为1,
故ABCD为正四面体,
连接BO并延长,交CD于F,
以F为坐标原点建立如图所示的空间坐标系: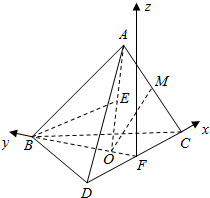
则F(0,0,0),B(0,$\frac{\sqrt{3}}{2}$,0),O(0,$\frac{\sqrt{3}}{6}$,0),A(0,$\frac{\sqrt{3}}{6}$,$\frac{\sqrt{6}}{3}$),
E(0,$\frac{\sqrt{3}}{6}$,$\frac{\sqrt{6}}{6}$),C($\frac{1}{2}$,0,0),M($\frac{1}{4}$,$\frac{\sqrt{3}}{12}$,$\frac{\sqrt{6}}{6}$),
∴$\overrightarrow{OM}$=($\frac{1}{4}$,-$\frac{\sqrt{3}}{12}$,$\frac{\sqrt{6}}{6}$),$\overrightarrow{BE}$=(0,-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{6}$),
设异面直线OM与BE所成的角为θ,
则cosθ=$\frac{|\overrightarrow{OM}•\overrightarrow{BE}|}{\left|\overrightarrow{OM}\right|•\left|\overrightarrow{BE}\right|}$=$\frac{\frac{1}{4}}{\frac{1}{2}×\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}}{2}$,
故异面直线OM与BE所成的角为:$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题考查的知识点是空间异面直线的夹角,建立空间坐标系,将异面直线夹角转化为向量夹角,是解答的关键.

 优生乐园系列答案
优生乐园系列答案| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |