题目内容
5.设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为( )| A. | $\root{3}{4V}$ | B. | $\root{3}{6V}$ | C. | $\root{3}{8V}$ | D. | $\sqrt{4V}$ |
分析 设底边边长为a,高为h,利用体积公式V=Sh得出h,再根据表面积公式得S=$\frac{\sqrt{3}}{2}$a2+$\frac{4\sqrt{3}V}{a}$,最后利用导函数即得底面边长.
解答 解:设底边边长为a,高为h,
则V=Sh=$\frac{\sqrt{3}}{4}$a2×h,
∴h=$\frac{4\sqrt{3}V}{3{a}^{2}}$,
则表面积为S=3ah+2•$\frac{\sqrt{3}}{4}$a2=$\frac{\sqrt{3}}{2}$a2+$\frac{4\sqrt{3}V}{a}$,
则S′=$\sqrt{3}$a-$\frac{4\sqrt{3}V}{{a}^{2}}$,
令$\sqrt{3}$a-$\frac{4\sqrt{3}V}{{a}^{2}}$=0可得a=$\root{3}{4V}$.
故选:A
点评 本小题主要考查棱柱、棱锥、棱台、棱柱、棱锥、棱台的侧面积和表面积、基本不等式等基础知识,考查运算求解能力,考查转化思想.属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
13.若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连结正方体各顶点的所有直线中,“黄金异面直线对”共有( )
| A. | 48对 | B. | 24对 | C. | 12对 | D. | 66对 |

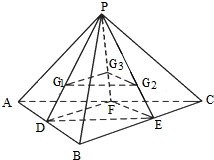 已知P为△ABC所在平面外一点,G1、G2、G3分别是△PAB、△PCB、△PAC的重心;D、E、F分别是AB、BC、CA的中点.
已知P为△ABC所在平面外一点,G1、G2、G3分别是△PAB、△PCB、△PAC的重心;D、E、F分别是AB、BC、CA的中点. 如图,三棱柱 ABC-A1 B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱 ABC-A1 B1C1中,CA=CB,AB=AA1,∠BAA1=60°. 如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.