题目内容
3. 如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )
如图,PA切圆O于点A,割线PBC经过圆心O,若PB=OB=1,OD平分∠AOC,交圆O于点D,连接PD交圆O于点E,则PE的长等于( )| A. | $\frac{{\sqrt{7}}}{7}$ | B. | $\frac{{3\sqrt{7}}}{7}$ | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\sqrt{7}$ |
分析 先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
解答 解:由题意,PB=OB=1,PA切圆O于点A,所以∠AOB=60°,
因为OD平分∠AOC,所以∠AOD=60°,
所以∠POD=120°,
由余弦定理得,PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2×(-$\frac{1}{2}$)=7,
所以PD=$\sqrt{7}$.
根据割线定理PE•PD=PB•PC得,$\sqrt{7}$PE=1×3,
所以PE=$\frac{3\sqrt{7}}{7}$
故选:B.
点评 已知三角形两边与夹角时,一定要想到余弦定理的运用,之后做题的思路也许会豁然开朗.

练习册系列答案
相关题目
13.若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连结正方体各顶点的所有直线中,“黄金异面直线对”共有( )
| A. | 48对 | B. | 24对 | C. | 12对 | D. | 66对 |
11.某程序框图如图所示,该程序运行后输出S的值是( )
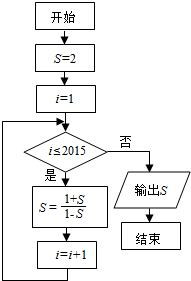

| A. | $\frac{1}{3}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
 如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.