题目内容
4.已知正方形ABCD的边长是4,若将△BCD沿正方形的对角线BD所在的直线进行翻折,则在翻折过程中,四面体C-ABD的体积的最大值是$\frac{{16\sqrt{2}}}{3}$.分析 当平面BCD⊥平面ABD时,三棱锥C-ABD的高最大为CO,利用正方形的性质与三棱锥的体积计算公式即可得出.
解答 解:如图所示,
当平面BCD⊥平面ABD时,三棱锥C-ABD的高最大为CO,
∴VC-ABD=$\frac{1}{3}OC•{S}_{△ABD}$=$\frac{1}{3}×2\sqrt{2}×\frac{1}{2}×{4}^{2}$=$\frac{{16\sqrt{2}}}{3}$.
故答案为:$\frac{16\sqrt{2}}{3}$.
点评 本题主要考查了正方形的性质与三棱锥的体积计算公式等基础知识,考查空间想象能力、推理论证能力、运算求解能力、化归与转化能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连结正方体各顶点的所有直线中,“黄金异面直线对”共有( )
| A. | 48对 | B. | 24对 | C. | 12对 | D. | 66对 |
 如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱AB,A1D1,AD的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是棱AB,A1D1,AD的中点,求证:
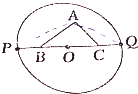 如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.
如图,Rt△ABC的斜边长为定值2cm,以斜边的中点O为圆心作半径为n的圆,BC的延长线交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.