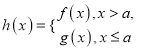Question

【题目】已知a，b∈R，若a2+b2﹣ab=1，则ab的取值范围是 ．

Answer 1

【答案】[ ，1]
【解析】解：当ab＞0时， ∵a，b∈R，且a2+b2﹣ab=1，
∴a2+b2=ab+1，
又a2+b2≥2ab当且仅当a=b时“=”成立；
∴ab+1≥2ab，
∴ab≤1，当且仅当a=b=±1时“=”成立；
即0＜ab≤1；
当ab=0时，不妨设a=0，则b=±1，满足题意；
当ab＜0时，
又∵a2+b2≥﹣2ab，
∴ab+1≥﹣2ab，
∴﹣3ab≤1，
∴ab≥﹣ ，
当且仅当a= ，b=﹣ ，或a=﹣ 、b= 时“=”成立；
即0＞ab≥﹣ ；
综上，ab的取值范围是[﹣ ，1]．
故答案为[ ，1]．
灵活应用基本不等式a2+b2≥2ab，即可求出ab的取值范围．