题目内容
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若对任意![]() ,均有
,均有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设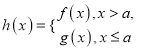 ,若
,若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)当a=0时, ![]() ,,借助换元法及二次函数图象及性质即可求函数g(x)的值域;
,,借助换元法及二次函数图象及性质即可求函数g(x)的值域;
(2)分类讨论,|f(x)|≤2,可化为![]() ,变量分离,构建新函数求最值,即可求a的取值范围;
,变量分离,构建新函数求最值,即可求a的取值范围;
(3)分类讨论,利用配方法,结合![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
试题解析:
(1)当![]() 时,
时, ![]() ,
,
因为![]() ,
,
所以![]() ,
, ![]() 的值域为
的值域为![]()
(2)若![]() ,
, ![]()
若![]() 时,
时, ![]() 可化为
可化为![]()
即![]() ,所以
,所以![]()
因为![]() 在
在![]() 为递增函数,所以函数
为递增函数,所以函数![]() 的最大值为
的最大值为![]() ,
,
因为![]() (当且仅当
(当且仅当![]() ,即
,即![]() 取“
取“![]() ”)
”)
所以![]() 的取值范围是
的取值范围是![]() .
.
(3)因为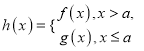 当
当![]() 时,
时, ![]() ,
,
令![]() ,
, ![]() ,则
,则![]()
![]() ,
,
当![]() 时,即
时,即![]() ,
, ![]() ;
;
当![]() 时,
时, ![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
, 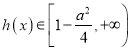 .
.
若![]() ,
, ![]() ,此时
,此时![]() ,
,
若![]() ,即
,即![]() ,此时
,此时![]() ,所以实数
,所以实数![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目