题目内容
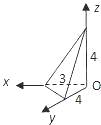
【题目】正四棱锥P﹣ABCD，B1为PB的中点，D1为PD的中点，则两个棱锥A﹣B1CD1 ， P﹣ABCD的体积之比是（ ）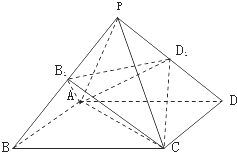 
A.1：4
B.3：8
C.1：2
D.2：3
【答案】A
【解析】解答：如图，棱锥A﹣B1CD1 ， 的体积可以看成是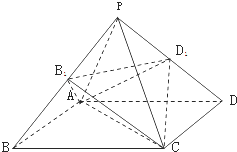 
正四棱锥P﹣ABCD的体积减去角上的四个小棱锥的体积得到，
因为B1为PB的中点，D1为PD的中点，
∴棱锥B1﹣ABC，的体积和棱锥D1﹣ACD，的体积都是正四棱锥P﹣ABCD的体积的 
，
棱锥C﹣PB1D1 ， 的体积与棱锥A﹣PB1D1的体积之和是正四棱锥P﹣ABCD的体积的 ，
则中间剩下的棱锥A﹣B1CD1的体积
=正四棱锥P﹣ABCD的体积﹣3× 
个正四棱锥P﹣ABCD的体积
= 个正四棱锥P﹣ABCD的体积
则两个棱锥A﹣B1CD1 ， P﹣ABCD的体积之比是1：4．
故选A．
分析：如图，棱锥A﹣B1CD1 ， 的体积可以看成正四棱锥P﹣ABCD的体积减去角上的四个小棱锥的体积得到，利用底面与高之间的关系得出棱锥B1﹣ABC，的体积和棱锥D1﹣ACD，的体积都是正四棱锥P﹣ABCD的体积的 ，棱锥C﹣PB1D1 ， 的体积与棱锥A﹣PB1D1的体积之和是正四棱锥P﹣ABCD的体积的 ，则中间剩下的棱锥A﹣B1CD1的体积=正四棱锥P﹣ABCD的体积﹣3× 个正四棱锥P﹣ABCD的体积，最终得到则两个棱锥A﹣B1CD1 ， P﹣ABCD的体积之比．
练习册系列答案
阅读快车系列答案
相关题目
