题目内容
【题目】设命题p：（4x﹣3）2≤1；命题q：x2﹣（2a+1）x+a（a+1）≤0，若￢p是￢q的必要不充分条件，求实数a的取值范围．
【答案】解：设A={x|（4x﹣3）2≤1}，B={x|x2﹣（2a+1）x+a（a+1）≤0}，
易知A={x| 
≤x≤1}，B={x|a≤x≤a+1}．
由p是q的必要不充分条件，从而p是q的充分不必要条件，即AB，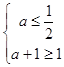
且两等号不能同时取．
故所求实数a的取值范围是[0， ]．
【解析】分别解出命题p和命题q中不等式的解集得到集合A和集合B，根据p是q的必要不充分条件，得到q是p的必要不充分条件，即q推不出p，而p能推出q．说明P的解集被q的解集包含，即集合A为集合B的真子集，列出关于a的不等式，求出不等式的解集即可得到a的取值范围．
练习册系列答案
相关题目
