Question

【题目】在正方形ABCD中，AB=AD=2，M，N分别是边BC，CD上的动点，且MN= ，则 的取值范围为 ．

Answer 1

【答案】[4，8﹣2 ]
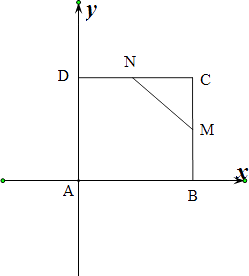
【解析】解：以AB，AD为坐标轴建立平面直角坐标系如图：
设CM=a，则CN= ．∴0 ．
∴M（2，2﹣a），N（2﹣ ，2）．
∴ =（2，2﹣a）， =（2﹣ ，2）．
∴ =4﹣2 +4﹣2a=8﹣2（a+ ）．
∵2a ≤a2+（ ）2=2，
∴（a+ ）2=2+2a ≤4．
∴a+ ≤2．
又由三角形的性质可得MC+CN＞MN= ，当M，C，N三点共线时，MC+CN=MN= ．
∴ a+ ≤2．
∴当a+ = 时， 取得最大值8﹣2 ，当a+ =2时， 取得最小值4．
所以答案是：[4，8﹣2 ]．