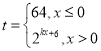题目内容
【题目】(1)已知全集U={2,4,a2-a+1},A={a+4,4},UA={7},则a=________.
(2)当a>0且a≠1时,函数![]() 必过定点_______
必过定点_______
(3)为了保证信息安全,传输必须使用加密方式,有一种方式其加密、解密原理如下:
明文![]() 密文
密文![]() 密文
密文![]() 明文
明文
己知加密为y=ax-2(x为明文、y为密文),如果明文“3”通过加密后得到密文为“6”,再发送,接收方通过解密得到明文“3”,若接收方接到密文为“14”,则原发的明文是________.
(4)已知3a=5b=M,且![]() ,则M的值为______________。
,则M的值为______________。
【答案】-2 (2,-2) 4 ![]()
【解析】
(1)由UA={7},可得a2-a+1=7,解得a再检验即可得解;
(2)令![]() 即可得定点;
即可得定点;
(3)由,x=3时,y=6,代入条件可得函数解析式,再令y=14,求解x即可;
(4)由题意可知![]() ,再代入条件,利用换底公式即可得解.
,再代入条件,利用换底公式即可得解.
(1)解:已知全集U={2,4,a2-a+1},A={a+4,4},UA={7},
∴a2-a+1=7,解得a=-2,或a=3,
当a=3时,a+4=7,∴A={7,4},不合题意舍去,
∴a=-2.
故答案为-2.
(2)解:当a>0且a≠1时,函数![]() ,当x=2时,f(2)=a0-3=-2,
,当x=2时,f(2)=a0-3=-2,
∴函数![]() 必过定点(2,-2).
必过定点(2,-2).
故答案为(2,-2).
(3)由题意,对于y=ax-2中,x=3时,y=6,即a3-2=6,解得a=2,
∴函数y=2x-2,当y=14时,有2x-2=14,解得x=4.
即原发的明文是4.
故答案为4.
(4)解:∵3a=5b=M,∴![]() .,
.,
代入![]() ,得
,得![]() ,则
,则![]() ,
,
∴![]() ,解得M=
,解得M=![]() .
.
故答案为![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目