题目内容
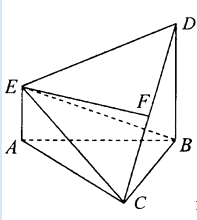
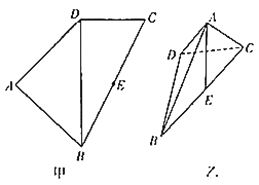
【题目】如图甲,四边形![]() 中,
中,![]() 是
是![]() 的中点,
的中点, ![]() .将(图甲)沿直线
.将(图甲)沿直线![]() 折起,使二面角
折起,使二面角![]() 为
为![]() (如图乙).
(如图乙).
(1)求证:![]() ⊥平面
⊥平面![]()
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,可知
,可知![]() ,
,![]() 平面
平面![]() ,即
,即![]() ,也可证明
,也可证明![]() ,根据线面垂直的判断定理可证
,根据线面垂直的判断定理可证![]() 平面
平面![]() ;(2)根据等体积转化
;(2)根据等体积转化![]() ,可得点到平面的距离,或是利用空间直角坐标解决.
,可得点到平面的距离,或是利用空间直角坐标解决.
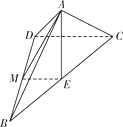
试题解析:(Ⅰ)证明:如图,取BD中点M,连接AM,ME.
![]()
因为AB=AD=![]() ,所以AM⊥BD, 因为DB=2,DC=1,BC=
,所以AM⊥BD, 因为DB=2,DC=1,BC=![]() ,满足:DB 2+DC 2=BC 2, 所以△BCD是以BC为斜边的直角三角形,BD⊥DC,因为E是BC的中点,所以ME为△BCD的中位线,
,满足:DB 2+DC 2=BC 2, 所以△BCD是以BC为斜边的直角三角形,BD⊥DC,因为E是BC的中点,所以ME为△BCD的中位线,![]() ME∥
ME∥![]() ,
,![]() ME⊥BD,ME=
ME⊥BD,ME=![]()
![]() ∠AME是二面角A-BD-C的平面角,
∠AME是二面角A-BD-C的平面角,![]() =
=![]() °.
°.
![]() ,
,![]() 且AM、ME是平面AME内两条相交于点M的直线,
且AM、ME是平面AME内两条相交于点M的直线,
![]() ,
,![]() 平面AEM,
平面AEM,![]() .
.
![]() ,
,![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,在△AME中,由余弦定理得:
,在△AME中,由余弦定理得:
![]()
![]()
![]() ,
,![]() .
.
(Ⅱ)解法一:等体积法.
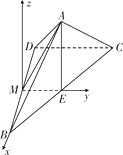
解法二:如图5,以M为原点,MB所在直线为x轴,ME所在直线为y轴,
平行于EA的直线为z轴,建立空间直角坐标系,
则由(Ⅰ)及已知条件可知B(1,0,0),![]() ,
,![]() ,D
,D![]() ,C
,C![]() .则
.则![]()
![]() 设平面ACD的法向量为
设平面ACD的法向量为![]() =
=![]() ,
,
则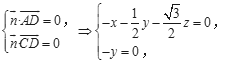 令
令![]() 则z=-2,
则z=-2,![]()
![]() 到平面
到平面![]() 的距离为d,则
的距离为d,则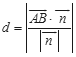 ,所以d
,所以d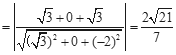 .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目