已知f(x)在R上可导.且满足≥0.则f≥(填两个数值的大小关系:＞.=.＜.≥.≤)．题目和参考答案——青夏教育精英家教网—

题目内容

17．已知f（x）在R上可导，且满足（x-2）f′（x）≥0，则f（-2015）+f（2015）≥（大于等于）2f（2）（填两个数值的大小关系：＞、=、＜、≥、≤）．

分析根据条件判断函数的单调性，利用函数的单调性进行比较即可．

解答解：当x＞2时，f′（x）≥0时，函数为增函数，
当x＜2时，f′（x）≤0时，函数为减函数，
即当x=2时，函数为极小值同时也是最小值，
故f（2015）≥f（2），
f（-2015）≥f（2），
则f（2015）+f（2015）≥2f（2），
故答案为：≥．

点评本题主要考查函数值的大小比较，求函数的导数，利用导数研究函数的单调性是解决本题的关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

7．

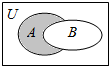集合U=R，A={x|x²-x-2＜0}，B={x|y=ln（1-x）}，则图中阴影部分表示的集合是（　　）

	A．	0与{0}表示同一个集合
	B．	由1，2，3组成的集合可表示为{1，2，3}或{3，2，1}
	C．	方程（x-1）²（x-2）=0的所有解的集合可表示为{1，1，2}
	D．	集合{x\|4＜x＜5}是有限集

5．把sin$\frac{π}{12}$，sin$\frac{5}{12}π$，cos$\frac{5}{7}π$，tan$\frac{5}{12}π$由小到大排列为$cos\frac{5π}{7}$＜$sin\frac{π}{12}$＜$sin\frac{5}{12}π$＜$tan\frac{5}{12}π$．

12．已知函数f（x）=mx²-x+lnx．
（1）当m=-1时，求f（x）的极大值；
（2）若在函数f（x）的定义域内存在区间D，使得该函数在区间D上为减函数，求实数m的取值范围；
（3）当$0＜m≤\frac{1}{2}$时，若曲线C：y=f（x）在点x=1处的切线l与曲线C有且只有一个公共点，求m的值或取值范围．

2．函数f（x）=3^x|${log_{\frac{1}{3}}}$x|-1的零点个数为2•

9．设函数f（x）是定义在R上的奇函数，且对任意x∈R都有f（x）=f（x+4），当，x∈（0，2）时，f（x）=2^x，则f（2015）的值为（　　）

6．函数f（x）=a^x-1+2的图象恒过一定点，则这个定点坐标是（1，3）．

7．设函数f（x）=$\left\{\begin{array}{l}{asinx+2，x≥0}\\{{x}^{2}+2a，x＜0}\end{array}\right.$（其中a∈R）的值域为S，若[1，+∞）⊆S，则a的取值范围是（　　）

A．

（-∞，$\frac{1}{2}$）

B．

[1，$\frac{3}{2}$]∪（$\frac{7}{4}$，2]

C．

（-∞，$\frac{1}{2}$）∪[1，2]

D．

（$\frac{3}{2}$，+∞）

试题分类