题目内容
(本小题满分14分)
证明以下命题:
(1)对任一正整数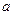 ,都存在正整数
,都存在正整数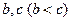 ,使得
,使得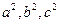 成等差数列;
成等差数列;
(2)存在无穷多个互不相似的三角形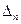 ,其边长
,其边长 为正整数且
为正整数且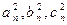 成等差数列.
成等差数列.
证明以下命题:
(1)对任一正整数
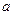 ,都存在正整数
,都存在正整数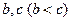 ,使得
,使得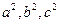 成等差数列;
成等差数列;(2)存在无穷多个互不相似的三角形
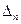 ,其边长
,其边长 为正整数且
为正整数且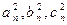 成等差数列.
成等差数列. (1)见解析(2)见解析
证明:(1)易知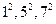 成等差数列,故
成等差数列,故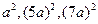 也成等差数列,
也成等差数列,
所以对任一正整数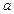 ,都存在正整数
,都存在正整数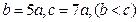 ,使得
,使得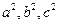 成等差数列.
成等差数列.
(2)若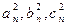 成等差数列,则有
成等差数列,则有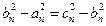 ,
,
即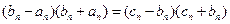 …… ①
…… ①
选取关于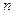 的一个多项式,例如
的一个多项式,例如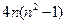 ,使得它可按两种方式分解因式,由于
,使得它可按两种方式分解因式,由于
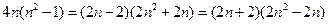
因此令 ,可得
,可得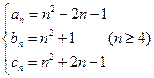 …… ②
…… ②
易验证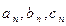 满足①,因此
满足①,因此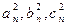 成等差数列,
成等差数列,
当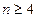 时,有
时,有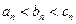 且
且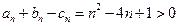
因此 为边可以构成三角形.
为边可以构成三角形.
其次,任取正整数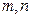
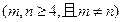 ,假若三角形
,假若三角形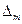 与
与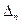 相似,则有:
相似,则有:
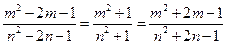 ,据比例性质有:
,据比例性质有:
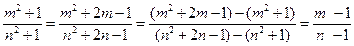

所以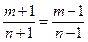 ,由此可得
,由此可得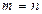 ,与假设
,与假设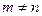 矛盾,
矛盾,
即任两个三 角形
角形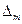 与
与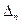
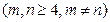 互不相似,
互不相似,
所以存在无穷多个互不相似的三角形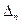 ,其边长
,其边长 为正整数且
为正整数且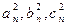 成等差数列.
成等差数列.
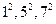 成等差数列,故
成等差数列,故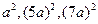 也成等差数列,
也成等差数列,所以对任一正整数
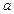 ,都存在正整数
,都存在正整数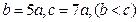 ,使得
,使得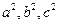 成等差数列.
成等差数列.(2)若
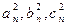 成等差数列,则有
成等差数列,则有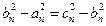 ,
,即
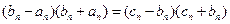 …… ①
…… ①选取关于
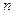 的一个多项式,例如
的一个多项式,例如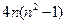 ,使得它可按两种方式分解因式,由于
,使得它可按两种方式分解因式,由于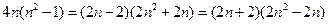
因此令
 ,可得
,可得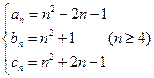 …… ②
…… ②易验证
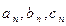 满足①,因此
满足①,因此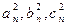 成等差数列,
成等差数列,当
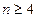 时,有
时,有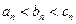 且
且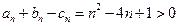
因此
 为边可以构成三角形.
为边可以构成三角形.其次,任取正整数
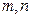
 ,假若三角形
,假若三角形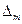 与
与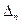 相似,则有:
相似,则有: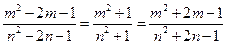 ,据比例性质有:
,据比例性质有: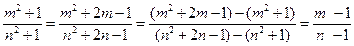

所以
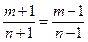 ,由此可得
,由此可得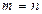 ,与假设
,与假设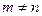 矛盾,
矛盾,即任两个三
 角形
角形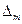 与
与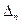
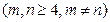 互不相似,
互不相似,所以存在无穷多个互不相似的三角形
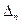 ,其边长
,其边长 为正整数且
为正整数且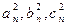 成等差数列.
成等差数列.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
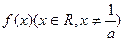 满足
满足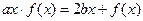 ,
,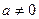 ,
,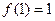 ;且使
;且使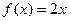 成立的实数
成立的实数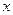 只有一个。
只有一个。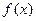 的表达式;
的表达式;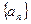 满足
满足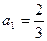 ,
,
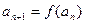 ,
,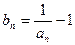 ,
,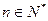 ,证明数列
,证明数列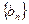 是等比数列,并求出
是等比数列,并求出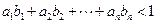 ,
,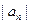 为等差数列,且
为等差数列,且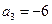 ,
, 。
。 (Ⅱ)若等差数列
(Ⅱ)若等差数列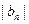 满足
满足 ,
, ,求
,求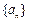 的前n项和
的前n项和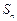 满足:
满足: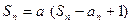 (
(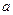 为常数,
为常数,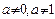 )(Ⅰ)求
)(Ⅰ)求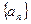 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设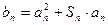 ,若数列
,若数列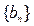 为等比数列,求
为等比数列,求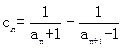 ,数列
,数列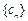 的前n项和为
的前n项和为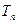 . 求证:
. 求证: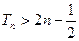 .
.
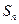 为等差数列
为等差数列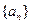 的前
的前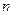 项和,若
项和,若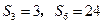 ,则
,则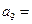 。
。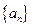 满足
满足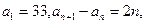 则
则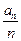 的最小值为__________.
的最小值为__________.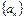 的前
的前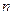 项和
项和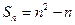 ,则这个数列的通项公式为--( )
,则这个数列的通项公式为--( )


