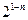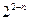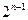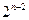题目内容
已知函数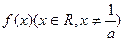 满足
满足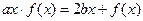 ,
,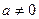 ,
,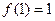 ;且使
;且使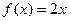 成立的实数
成立的实数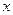 只有一个。
只有一个。
(Ⅰ)求函数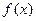 的表达式;
的表达式;
(Ⅱ)若数列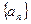 满足
满足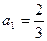 ,
,
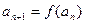 ,
,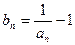 ,
,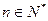 ,证明数列
,证明数列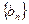 是等比数列,并求出
是等比数列,并求出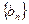 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,证明: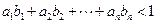 ,
,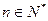
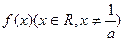 满足
满足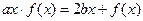 ,
,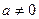 ,
,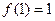 ;且使
;且使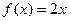 成立的实数
成立的实数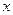 只有一个。
只有一个。(Ⅰ)求函数
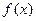 的表达式;
的表达式;(Ⅱ)若数列
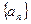 满足
满足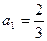 ,
,
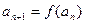 ,
,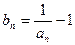 ,
,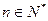 ,证明数列
,证明数列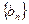 是等比数列,并求出
是等比数列,并求出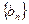 的通项公式;
的通项公式;(Ⅲ)在(Ⅱ)的条件下,证明:
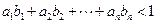 ,
,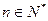
(I)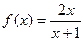
(II)见解析通项公式为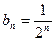
(Ⅲ)见解析
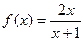
(II)见解析通项公式为
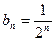
(Ⅲ)见解析
(Ⅰ)由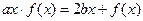 ,
,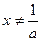 ,
,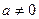 ,得
,得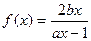 .………1分
.………1分
由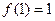 ,得
,得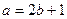 .……………………………………………………………2分
.……………………………………………………………2分
由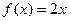 只有一解,即
只有一解,即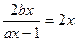 ,也就是
,也就是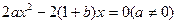 只有一解,
只有一解,
∴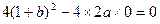
∴ .…………………………………………………………………………………3分
.…………………………………………………………………………………3分
∴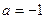 .故
.故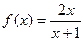 .……………………………………………………………4分
.……………………………………………………………4分
(Ⅱ)∵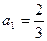 ,
,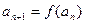 ,∴
,∴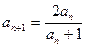 ………………………… 5分
………………………… 5分
∴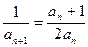 ……………………………………………………………6分
……………………………………………………………6分

∴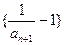 是以
是以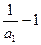 =
=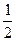 为首项,
为首项,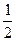 为公比的等比数列
为公比的等比数列
∴有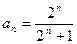 ………………………8分
………………………8分
∵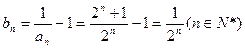 ,∴
,∴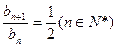
∴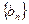 是首项为
是首项为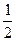 ,公比为
,公比为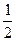 的等比数列,其通项公式为
的等比数列,其通项公式为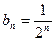 .……………10分
.……………10分
(Ⅲ)∵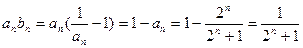 ,
,
∴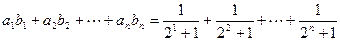 …………………………12分
…………………………12分
 .……………………………15分
.……………………………15分
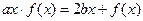 ,
,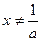 ,
,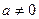 ,得
,得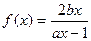 .………1分
.………1分由
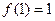 ,得
,得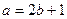 .……………………………………………………………2分
.……………………………………………………………2分由
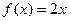 只有一解,即
只有一解,即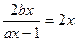 ,也就是
,也就是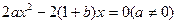 只有一解,
只有一解,∴
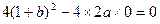
∴
 .…………………………………………………………………………………3分
.…………………………………………………………………………………3分∴
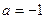 .故
.故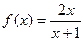 .……………………………………………………………4分
.……………………………………………………………4分(Ⅱ)∵
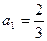 ,
,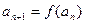 ,∴
,∴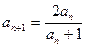 ………………………… 5分
………………………… 5分∴
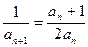 ……………………………………………………………6分
……………………………………………………………6分
∴
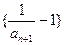 是以
是以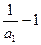 =
=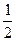 为首项,
为首项,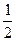 为公比的等比数列
为公比的等比数列∴有
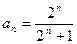 ………………………8分
………………………8分∵
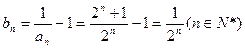 ,∴
,∴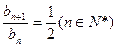
∴
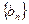 是首项为
是首项为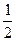 ,公比为
,公比为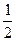 的等比数列,其通项公式为
的等比数列,其通项公式为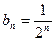 .……………10分
.……………10分(Ⅲ)∵
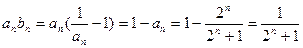 ,
,∴
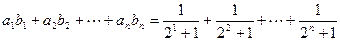 …………………………12分
…………………………12分 .……………………………15分
.……………………………15分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
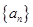 的首项
的首项 ,其前
,其前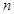 项的和为
项的和为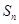 ,且
,且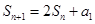 ,则
,则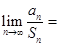
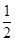
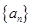 中,
中,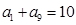 ,则
,则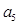 的值为
的值为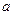 ,都存在正整数
,都存在正整数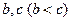 ,使得
,使得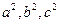 成等差数列;
成等差数列;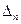 ,其边长
,其边长 为正整数且
为正整数且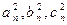 成等差数列.
成等差数列. 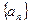 的前
的前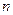 项和为
项和为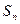 ,已知
,已知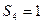 ,
,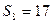 , 求数列
, 求数列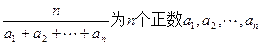 的“均倒数”,数列
的“均倒数”,数列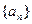 的各项均为正数,且其前
的各项均为正数,且其前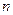 项的“均倒数”为
项的“均倒数”为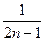 ,则数列
,则数列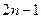
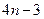
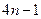
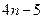
 为等差数列,
为等差数列,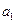 +
+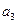 +
+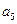 =105,
=105, =99,以
=99,以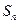 表示
表示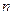 项和,则使得
项和,则使得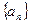 中,
中, 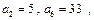 则
则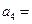 _________.
_________.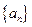 中
中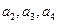 分别是某等差数列的第5项、第3 项、第2项,且
分别是某等差数列的第5项、第3 项、第2项,且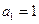 公比
公比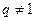 ,则
,则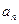 等于( )
等于( )