题目内容
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(1)求f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最值.
【答案】
(1)解:设x∈[0,1],则﹣x∈[﹣1,0].∴f(x)= ![]() =4x﹣2x
=4x﹣2x
又∵f(﹣x)=﹣f(x)=﹣(4x﹣2x)∴f(x)=2x﹣4x.
所以,f(x)在[0,1]上的解析式为f(x)=2x﹣4x
(2)解:当x∈[0,1],f(x)=2x﹣4x=﹣(2x)2+2x,
∴设t=2x(t>0),则y=﹣t2+t∵x∈[0,1],∴t∈[1,2]
当t=1时x=0,f(x)max=0;当t=2时x=1,f(x)min=﹣2
【解析】(1)设x∈[0,1],则﹣x∈[﹣1,0],利用条件结合奇函数的定义求f(x)在[0,1]上的解析式;(2)设t=2x(t>0),则y=﹣t2+t,利用二次函数的性质求f(x)在[0,1]上的最值.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及下面一些统计量的值.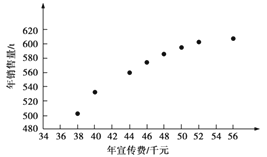
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中 ![]() ,
, ![]() .
.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最下二乘估计分别为 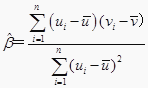 ,
, ![]() .
.
(1)根据散点图判断,y=a+bx与 ![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:
①年宣传费x=49时,年销售量及年利润的预报值时多少?
②年宣传费x为何值时,年利润的预报值最大?