题目内容
(本题满分14分)在数列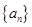 中,
中,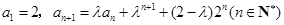 ,其中
,其中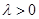 .
.
(Ⅰ)求数列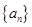 的通项公式;
的通项公式;
(Ⅱ)求数列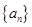 的前
的前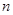 项和
项和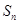 ;
;
(Ⅲ)证明存在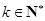 ,使得
,使得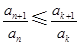 对任意
对任意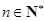 均成立.
均成立.
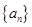 中,
中,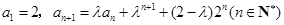 ,其中
,其中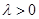 .
.(Ⅰ)求数列
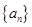 的通项公式;
的通项公式;(Ⅱ)求数列
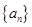 的前
的前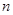 项和
项和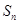 ;
;(Ⅲ)证明存在
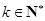 ,使得
,使得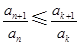 对任意
对任意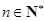 均成立.
均成立.解:(Ⅰ)解法一: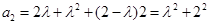 ,
,  ,
,
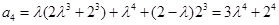 .由此可猜想出数列
.由此可猜想出数列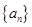 的通项公式为
的通项公式为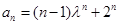 .
.
以下用数学归纳法证明.
(1)当 时,
时,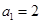 ,等式成立.
,等式成立.
(2)假设当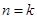 时等式成立,即
时等式成立,即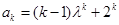 ,
,
那么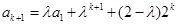
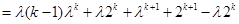
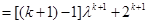 .
.
这就是说,当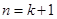 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式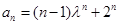 对任何
对任何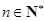 都成立.
都成立.
解法二:由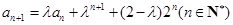 ,
,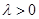 ,可得
,可得 ,
,
所以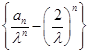 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故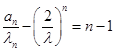 ,所以数列
,所以数列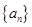 的通项公式为
的通项公式为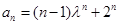 .
.
(Ⅱ)解:设 , ①
, ①
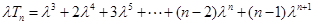 ②
②
当 时,①式减去②式,
时,①式减去②式,
得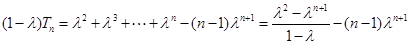 ,
,
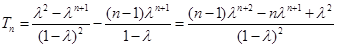 .
.
这时数列 的前
的前 项和
项和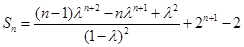 .
.
当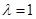 时,
时,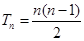 .这时数列
.这时数列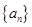 的前
的前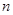 项和
项和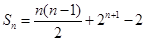 .
.
(Ⅲ)证明:通过分析,推测数列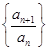 的第一项
的第一项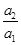 最大,下面证明:
最大,下面证明:
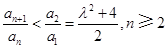 . ③
. ③
由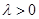 知
知 ,要使③式成立,只要
,要使③式成立,只要 ,
,
因为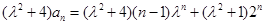
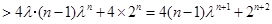
 .
.
所以③式成立.
因此,存在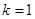 ,使得
,使得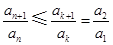 对任意
对任意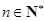 均成立.
均成立.
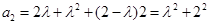 ,
,  ,
,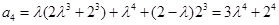 .由此可猜想出数列
.由此可猜想出数列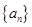 的通项公式为
的通项公式为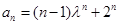 .
.以下用数学归纳法证明.
(1)当
 时,
时,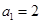 ,等式成立.
,等式成立.(2)假设当
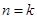 时等式成立,即
时等式成立,即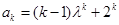 ,
,那么
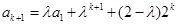
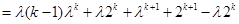
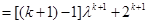 .
.这就是说,当
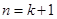 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式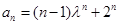 对任何
对任何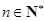 都成立.
都成立.解法二:由
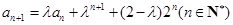 ,
,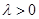 ,可得
,可得 ,
,所以
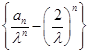 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故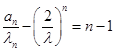 ,所以数列
,所以数列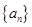 的通项公式为
的通项公式为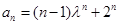 .
.(Ⅱ)解:设
 , ①
, ①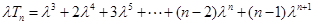 ②
②当
 时,①式减去②式,
时,①式减去②式,得
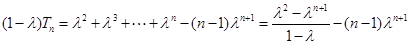 ,
,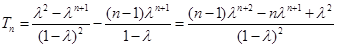 .
.这时数列
 的前
的前 项和
项和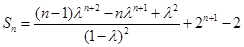 .
.当
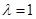 时,
时,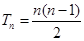 .这时数列
.这时数列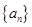 的前
的前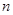 项和
项和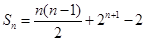 .
.(Ⅲ)证明:通过分析,推测数列
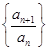 的第一项
的第一项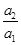 最大,下面证明:
最大,下面证明: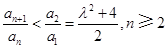 . ③
. ③由
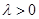 知
知 ,要使③式成立,只要
,要使③式成立,只要 ,
,因为
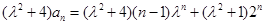
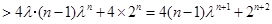
 .
.所以③式成立.
因此,存在
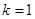 ,使得
,使得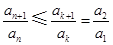 对任意
对任意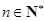 均成立.
均成立.略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
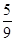 ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积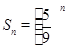 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=____________
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=____________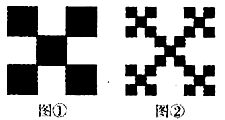
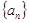 满足
满足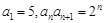 ,则
,则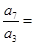 ( )
( )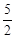
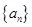 ,
,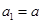 ,且
,且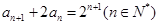 ,
,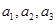 成等差数列,求实数
成等差数列,求实数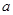 的值;(2)数列
的值;(2)数列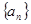 满足:
满足: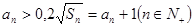 ,其中
,其中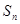 为
为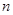 项和。
项和。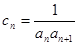 ,
,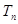 为
为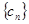 的前
的前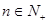 ,不等式
,不等式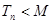 恒成立,求整数
恒成立,求整数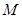 的最小值。
的最小值。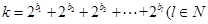 ,且
,且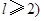 ,求m的最小值.
,求m的最小值.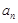 },
},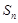 为其前n项的和,
为其前n项的和,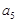 =6,
=6,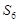 =18,n∈N*.
=18,n∈N*. I)求数列{
I)求数列{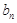 =3
=3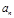 ,求数列{
,求数列{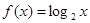 ,若
,若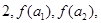
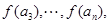
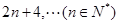 成等差数列.
成等差数列.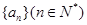 的通项公式;
的通项公式;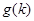 是不等式
是不等式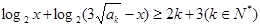 整数解的个数,求
整数解的个数,求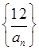 的前n项和为
的前n项和为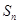 ,是否存在正数
,是否存在正数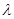 ,对任意正整数
,对任意正整数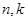 ,使
,使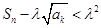 恒成立?若存在,求
恒成立?若存在,求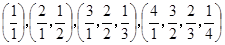 ,
,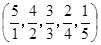 ,……
,……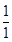 ,
,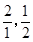 ,
,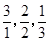 ,
,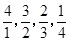 ,
,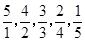
 ,……则此数列中的2012项是
,……则此数列中的2012项是