题目内容
(理)对数列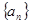 和
和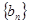 ,若对任意正整数
,若对任意正整数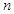 ,恒有
,恒有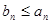 ,则称数列
,则称数列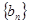 是数列
是数列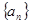 的“下界数列”.
的“下界数列”.
(1)设数列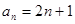 ,请写出一个公比不为1的等比数列
,请写出一个公比不为1的等比数列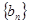 ,使数列
,使数列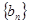 是数列
是数列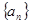 的“下界数列”;
的“下界数列”;
(2)设数列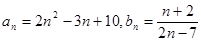 ,求证数列
,求证数列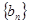 是数列
是数列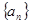 的“下界数列”;
的“下界数列”;
(3)设数列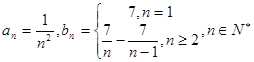 ,构造
,构造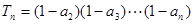 ,
,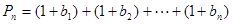 ,求使
,求使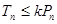 对
对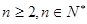 恒成立的
恒成立的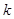 的最小值.
的最小值.
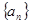 和
和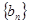 ,若对任意正整数
,若对任意正整数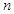 ,恒有
,恒有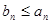 ,则称数列
,则称数列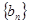 是数列
是数列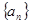 的“下界数列”.
的“下界数列”.(1)设数列
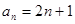 ,请写出一个公比不为1的等比数列
,请写出一个公比不为1的等比数列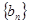 ,使数列
,使数列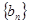 是数列
是数列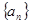 的“下界数列”;
的“下界数列”;(2)设数列
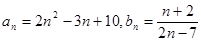 ,求证数列
,求证数列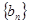 是数列
是数列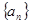 的“下界数列”;
的“下界数列”;(3)设数列
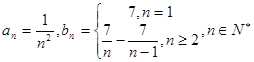 ,构造
,构造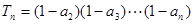 ,
,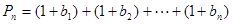 ,求使
,求使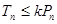 对
对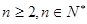 恒成立的
恒成立的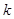 的最小值.
的最小值.(1)
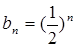 等,答案不唯一;……………4分
等,答案不唯一;……………4分(2)
 ,当
,当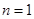 时
时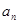 最小值为9,;……………6分
最小值为9,;……………6分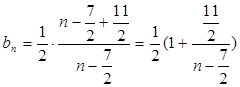 ,则
,则
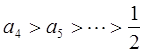 ,
,因此,
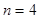 时,
时,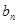 最大值为6,……………9分
最大值为6,……………9分所以,
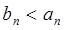 ,数列
,数列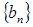 是数列
是数列 的“下界数列”;……………10分
的“下界数列”;……………10分(3)
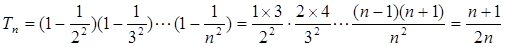 ,…11分
,…11分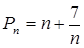 , ……………12分
, ……………12分不等式为
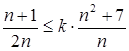 ,
,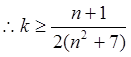 ,
,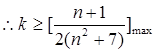 ,…13分
,…13分设
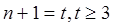 ,则
,则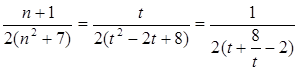 ,…………15分
,…………15分当
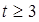 时,
时, 单调递增,
单调递增,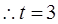 时,
时,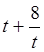 取得最小值,因此
取得最小值,因此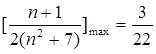 , ……………17分
, ……………17分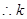 的最小值为
的最小值为 ……………18分
……………18分略

练习册系列答案
相关题目
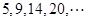 为“梯形数列”.根据图形的构成,此数列的第2012项与5的差,即
为“梯形数列”.根据图形的构成,此数列的第2012项与5的差,即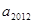 -5= .
-5= .


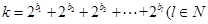 ,且
,且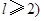 ,求m的最小值.
,求m的最小值.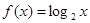 ,若
,若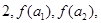
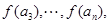
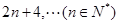 成等差数列.
成等差数列.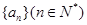 的通项公式;
的通项公式;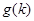 是不等式
是不等式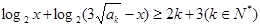 整数解的个数,求
整数解的个数,求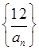 的前n项和为
的前n项和为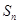 ,是否存在正数
,是否存在正数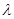 ,对任意正整数
,对任意正整数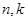 ,使
,使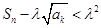 恒成立?若存在,求
恒成立?若存在,求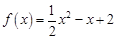 ,数列
,数列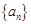 满足递推关系式:
满足递推关系式: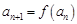 (
(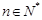 ),且
),且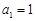 、
、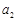 、
、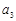 、
、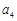 的值;
的值; 时,
时,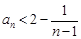 ;
;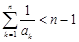 、
、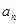 }中,
}中,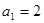 ,
,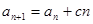 (
(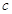 是不为0的常数,
是不为0的常数,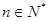 ),
),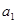 ,
,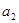 ,
,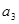 成等比数列.
成等比数列.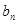 =
=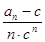 ,求数列{
,求数列{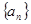 的前
的前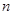 项和为
项和为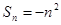 ,则( )
,则( )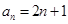
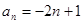
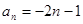
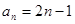
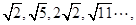 则
则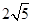 是这个数列的
是这个数列的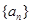 满足性质“对任意正整数
满足性质“对任意正整数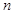 ,
,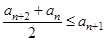 都成立”且
都成立”且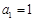 ,
,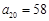 ,则
,则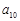 的最小值为
的最小值为