题目内容
.(本小题满分12分)已知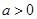 ,
,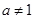 ,设
,设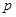 :函数
:函数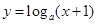 在
在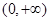 上单调递减;q:曲线
上单调递减;q:曲线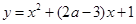 与x轴交于不同的两点,如果p且q为假命题,p或q为真命题,求实数a的取值范围.
与x轴交于不同的两点,如果p且q为假命题,p或q为真命题,求实数a的取值范围.
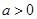 ,
,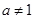 ,设
,设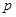 :函数
:函数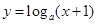 在
在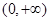 上单调递减;q:曲线
上单调递减;q:曲线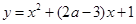 与x轴交于不同的两点,如果p且q为假命题,p或q为真命题,求实数a的取值范围.
与x轴交于不同的两点,如果p且q为假命题,p或q为真命题,求实数a的取值范围.解:由题意知p与q中 有且只有一个为真命题,…………………………2分
有且只有一个为真命题,…………………………2分
当0 < a < 1时,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;
当 ,函数
,函数 在(0,+∞)上不是单调递减;
在(0,+∞)上不是单调递减;
曲线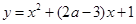 与x轴交于两点等价于
与x轴交于两点等价于 ,
,
即a < 或a >
或a >  .……………………………………4分
.……………………………………4分
(1)若p正确,q不正确,即函数 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,
曲线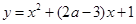 与x轴不交于两点,
与x轴不交于两点,
故a∈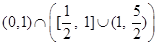 ,即a∈
,即a∈ .………………………7分
.………………………7分
(2)若p不正确,q正确,即函数 在(0,+∞)上不是单调递减,
在(0,+∞)上不是单调递减,
曲线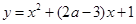 与x轴交于两点,因此a∈(1,+∞)∩((0,
与x轴交于两点,因此a∈(1,+∞)∩((0, )∪(
)∪( ,+∞)),
,+∞)),
即a∈( ,+∞).……………………………………………………………10分
,+∞).……………………………………………………………10分
综上,a取值范围为[ ,1)∪(
,1)∪( ,+∞).…………………………………………12分
,+∞).…………………………………………12分
 有且只有一个为真命题,…………………………2分
有且只有一个为真命题,…………………………2分当0 < a < 1时,函数
 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;当
 ,函数
,函数 在(0,+∞)上不是单调递减;
在(0,+∞)上不是单调递减;曲线
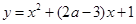 与x轴交于两点等价于
与x轴交于两点等价于 ,
,即a <
 或a >
或a >  .……………………………………4分
.……………………………………4分(1)若p正确,q不正确,即函数
 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,曲线
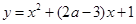 与x轴不交于两点,
与x轴不交于两点,故a∈
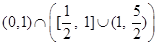 ,即a∈
,即a∈ .………………………7分
.………………………7分(2)若p不正确,q正确,即函数
 在(0,+∞)上不是单调递减,
在(0,+∞)上不是单调递减,曲线
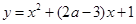 与x轴交于两点,因此a∈(1,+∞)∩((0,
与x轴交于两点,因此a∈(1,+∞)∩((0, )∪(
)∪( ,+∞)),
,+∞)),即a∈(
 ,+∞).……………………………………………………………10分
,+∞).……………………………………………………………10分综上,a取值范围为[
 ,1)∪(
,1)∪( ,+∞).…………………………………………12分
,+∞).…………………………………………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :关于
:关于 的函数
的函数 在[1,+∞)上是增函数,命题
在[1,+∞)上是增函数,命题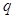 :关于
:关于 在R上为减函数,若
在R上为减函数,若 的取值范是 .
的取值范是 . ”的否定是 ▲
”的否定是 ▲  (1)
(1) 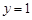 ;(2)
;(2)  ;(3)
;(3)  ;
;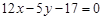
 “相关直线 ”的是 (只填序号)
“相关直线 ”的是 (只填序号)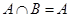 ”成立的必要条件是“
”成立的必要条件是“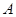
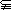
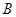 ”;
”;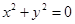 ,则
,则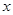 ,
,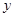 全为0”的否命题;
全为0”的否命题; ,则
,则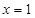 ”的逆否命题是“若
”的逆否命题是“若 ,则
,则 ”;
”; ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件; ”为假命题,则
”为假命题,则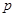 、
、 均为假命题;
均为假命题; ,使得
,使得 ,则
,则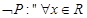 ,均有
,均有 ;
; ; (2)已知
; (2)已知 则
则 ;
; 的图象与函数
的图象与函数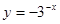 的图象关于原点对称;
的图象关于原点对称; 是偶函数;
是偶函数; 的递增区间为
的递增区间为 .
. 恒过定点
恒过定点 ,则焦点在y轴上且过点
,则焦点在y轴上且过点 .
. 与直线
与直线 垂直,则实数k=1;
垂直,则实数k=1; 对于任意
对于任意 ,有
,有 ,若
,若 ,则
,则 4
4 ,令
,令 为不大于
为不大于 ,则函数
,则函数 称为高斯函数或取整函数,若
称为高斯函数或取整函数,若 ,
, 为数列
为数列 的前
的前 项和,则
项和,则 145
145