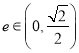题目内容
【题目】某网络购物平台每年11月11日举行“双十一”购物节,当天有多项优惠活动,深受广大消费者喜爱
(1)已知该网络购物平台近5年“双十”购物节当天成交额如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
成交额(百亿元) | 9 | 12 | 17 | 21 | 27 |
求成交额![]() (百亿元)与时间变量
(百亿元)与时间变量![]() (记2015年为
(记2015年为![]() ,2016年为
,2016年为![]() ,……依次类推)的线性回归方程,并预测2020年该平台“双十一”购物节当天的成交额(百亿元);
,……依次类推)的线性回归方程,并预测2020年该平台“双十一”购物节当天的成交额(百亿元);
(2)在2020年“双十一”购物节前,某同学的爸爸、妈妈计划在该网络购物平台.上分别参加![]() 、
、![]() 两店各一个订单的“秒杀”抢购,若该同学的爸爸、妈妈在
两店各一个订单的“秒杀”抢购,若该同学的爸爸、妈妈在![]() 、两店订单“秒杀”成功的概率分别为
、两店订单“秒杀”成功的概率分别为![]() 、
、![]() ,记该同学的爸爸和妈妈抢购到的订单总数量为
,记该同学的爸爸和妈妈抢购到的订单总数量为![]() .
.
(i)求![]() 的分布列及
的分布列及![]() ;
;
(ii)已知每个订单由![]() 件商品
件商品![]() 构成,记该同学的爸爸和妈妈抢购到的商品
构成,记该同学的爸爸和妈妈抢购到的商品![]() 总数量为
总数量为![]() ,假设
,假设 ,
, ,求
,求![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
【答案】(1)![]() ;30.7百亿元;(2)(i)分布列详见解析,
;30.7百亿元;(2)(i)分布列详见解析,![]() ;(ii)3.
;(ii)3.
【解析】
(1)计算![]() 、
、![]() ,求出系数
,求出系数![]() 和
和![]() ,写出线性回归方程,利用方程计算
,写出线性回归方程,利用方程计算![]() 时
时![]() 的值即可;
的值即可;
(2)![]() 由题意知随机变量
由题意知随机变量![]() 的可能取值,计算对应的概率值,写出分布列,求出数学期望值;
的可能取值,计算对应的概率值,写出分布列,求出数学期望值;
![]() 根据题意求出
根据题意求出![]() 的解析式,利用换元法和求导法计算
的解析式,利用换元法和求导法计算![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
解:(1)由已知可得:
![]() ,
,![]()
![]()
![]()
所以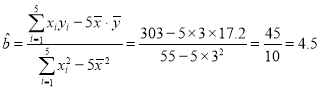
所以![]()
所以![]()
当![]() 时,
时,![]() (百亿元)
(百亿元)
所以估计2020年该平台“双十一”购物节当天的成交额为30.7(百亿元)
(2)(ⅰ)由题知,![]() 的可能取值为:0,1,2
的可能取值为:0,1,2
![]()
![]()
![]()
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
![]()
(ⅱ)因为![]()
所以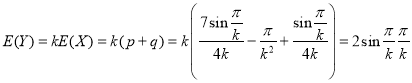
令![]() ,设
,设![]() ,则
,则![]()
因为![]() ,且
,且![]()
所以,当![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减;
上单调递减;
所以,当![]() 即
即![]() 时,
时,![]() (百亿元)
(百亿元)
所以![]() 取最大值时
取最大值时![]() 的值为3
的值为3

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案【题目】在2019年高考数学的全国Ⅲ卷中,文科和理科的选做题题目完全相同,第22题考查选修4-4:极坐标和参数方程;第23题考查选修4-5:不等式选讲.某校高三质量检测的命题采用了全国Ⅲ卷的形式,在测试结束后,该校数学组教师对该校全体高三学生的选做题得分情况进行了统计,得到两题得分的![]() 列联表如下(已知每名学生只做了一道题):
列联表如下(已知每名学生只做了一道题):
选做22题 | 选做23题 | 合计 | |
文科人数 | 50 | 60 | |
理科人数 | 40 | ||
总计 | 400 |
(1)完善![]() 列联表中的数据,判断能否有
列联表中的数据,判断能否有![]() 的把握认为“选做题的选择”与“文、理科的科类”有关;
的把握认为“选做题的选择”与“文、理科的科类”有关;
(2)经统计,第23题得分为0的学生中,理科生占理科总人数的![]() ,文科生占文科总人数的
,文科生占文科总人数的![]() ,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
,在按分层抽样的方法在第23题得分为0的学生中随机抽取6名进行单独辅导,并在辅导后随机抽取2名学生进行测试,求被抽中进行测试的2名学生均为理科生的概率.
附: ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |