题目内容
【题目】已知抛物线
：
的焦点为
，抛物线上的点到准线的最小距离为2.
（1）求抛物线的方程；
（2）若过点作互相垂直的两条直线
，
，与抛物线交于
，
两点，与抛物线交于，
两点，
，
分别为弦
，
的中点，求
的最小值.
【答案】（1）
；（2）32.
【解析】
（1）根据题意
，解得答案.
（2）设直线
的斜率为
，则直线
的斜率为
，联立方程解得
，
，则
，利用均值不等式得到答案.
（1）因为抛物线
上的点到准线的最小距离为2，所以，解得
，
故抛物线的方程为.
（2）焦点为
，
，所以两直线，的斜率都存在且均不为0.
设直线的斜率为，则直线的斜率为，
故直线的方程为
，联立方程组
消去
，整理得
.
设点
.
，则
.
因为
为弦的中点，所以
.
由
，得
，故点.
同理可得.
故
，
.
所以
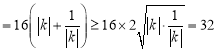，当且仅当
，即
时，等号成立.
所以
的最小值为32.
【题目】电动摩托车的续航里程，是指电动摩托车在蓄电池满电量的情况下一次能行驶的最大距离.为了解A，B两个不同型号电动摩托车的续航里程，现从某卖场库存电动摩托车中随机抽取A，B两个型号的电动摩托车各5台，在相同条件下进行测试，统计结果如下：
电动摩托车编号 | 1 | 2 | 3 | 4 | 5 |
A型续航里程（km） | 120 | 125 | 122 | 124 | 124 |
B型续航里程（km） | 118 | 123 | 127 | 120 | a |
已知A，B两个型号被测试电动摩托车续航里程的平均值相等.
（1）求a的值；
（2）求A型号被测试电动摩托车续航里程标准差的大小；
（3）从被测试的电动摩托车中随机抽取A，B型号电动摩托车各1台，求至少有1台的续航里程超过122km的概率.
（注：n个数据
，的方差
，其中
为数据的平均数）
【题目】某公司的甲、乙两名工程师因为工作需要，各自选购一台笔记本电脑.该公司提供了
三款笔记本电脑作为备选，这三款笔记本电脑在某电商平台的销量和用户评分如下表所示：
型号 |
|
|
|
销量（台） | 2000 | 2000 | 4000 |
用户评分 | 8 | 6.5 | 9.5 |
若甲选购某款笔记本电脑的概率与对应的销量成正比，乙选购某款笔记本电脑的概率与对应的用户评分减去5的值成正比，且他们两人选购笔记本电脑互不影响.
（1）求甲、乙两人选购不同款笔记本电脑的概率；
（2）若公司给购买这三款笔记本电脑的员工一定的补贴，补贴标准如下表：
型号 |
|
|
|
补贴（千元） | 3 | 4 | 5 |
记甲、乙两人获得的公司补贴之和为
千元，求的分布列和数学期望.