题目内容
【题目】医院为筛查某种疾病,需要血检,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,需要检验![]() 次;
次;
方式二:混合检验,把每个人的血样分成两份,取![]() 个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这
个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这![]() 个人只作一次检验就够了;如果结果是阳性,那么再对这
个人只作一次检验就够了;如果结果是阳性,那么再对这![]() 个人的另一份血样逐份检验,此时这
个人的另一份血样逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.
次.
(1)假设有6份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验岀来的概率;
(2)假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是相互独立的,且每份样本是阳性结果的概率为![]() .现取其中
.现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() (2)①
(2)①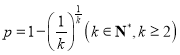 ②
②![]() 的最大值为12.
的最大值为12.
【解析】
(1)记恰好经过3次检验就能把阳性样本全部检验出来为![]() 事件,计算概率得到答案.
事件,计算概率得到答案.
(2)①计算![]() ,
,![]() ,根据
,根据![]() ,计算得到答案.
,计算得到答案.
②![]() ,所以
,所以![]() ,设
,设![]() ,求导得到单调区间,计算得到最值.
,求导得到单调区间,计算得到最值.
(1)记恰好经过3次检验就能把阳性样本全部检验出来为![]() 事件,
事件,
则![]() .
.
(2)①![]() 的取值为
的取值为![]() ,
,![]() ,所以
,所以![]() ,
,
![]() 的取值为1,
的取值为1,![]() ,计算
,计算![]() ,
,![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,所以
,所以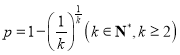 .
.
②![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() .
.
设![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
且![]() ,
,![]() ,
,
所以![]() 的最大值为12.
的最大值为12.

 阅读快车系列答案
阅读快车系列答案【题目】某网络购物平台每年11月11日举行“双十一”购物节,当天有多项优惠活动,深受广大消费者喜爱
(1)已知该网络购物平台近5年“双十”购物节当天成交额如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
成交额(百亿元) | 9 | 12 | 17 | 21 | 27 |
求成交额![]() (百亿元)与时间变量
(百亿元)与时间变量![]() (记2015年为
(记2015年为![]() ,2016年为
,2016年为![]() ,……依次类推)的线性回归方程,并预测2020年该平台“双十一”购物节当天的成交额(百亿元);
,……依次类推)的线性回归方程,并预测2020年该平台“双十一”购物节当天的成交额(百亿元);
(2)在2020年“双十一”购物节前,某同学的爸爸、妈妈计划在该网络购物平台.上分别参加![]() 、
、![]() 两店各一个订单的“秒杀”抢购,若该同学的爸爸、妈妈在
两店各一个订单的“秒杀”抢购,若该同学的爸爸、妈妈在![]() 、两店订单“秒杀”成功的概率分别为
、两店订单“秒杀”成功的概率分别为![]() 、
、![]() ,记该同学的爸爸和妈妈抢购到的订单总数量为
,记该同学的爸爸和妈妈抢购到的订单总数量为![]() .
.
(i)求![]() 的分布列及
的分布列及![]() ;
;
(ii)已知每个订单由![]() 件商品
件商品![]() 构成,记该同学的爸爸和妈妈抢购到的商品
构成,记该同学的爸爸和妈妈抢购到的商品![]() 总数量为
总数量为![]() ,假设
,假设 ,
, ,求
,求![]() 取最大值时正整数
取最大值时正整数![]() 的值.
的值.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
【题目】双十一购物狂欢节,是指每年11月11日的网络促销日,源于淘宝商城(天猫)2009年11月11日举办的网络促销活动,已成为中国电子商务行业的年度盛事.某生产商为了了解其生产的产品在不同电商平台的销售情况,统计了![]() 两个电商平台各十个网络销售店铺的销售数据:
两个电商平台各十个网络销售店铺的销售数据:
| 64 | 71 | 81 | 70 | 79 | 69 | 82 | 73 | 75 | 60 |
| 60 | 80 | 97 | 77 | 96 | 87 | 76 | 83 | 94 | 96 |
(1)作出![]() 两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
(2)填写下面关于店铺个数的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为销售量与电商平台有关;
的把握认为销售量与电商平台有关;
销售量 | 销售量 | 总计 | |
| |||
| |||
总计 |
(3)生产商要从这20个网络销售店铺销售量前五名的店铺中,随机抽取三个店铺进行销售返利,则其中恰好有两个店铺的销售量在95以上的概率是多少?
附: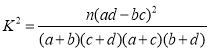 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |