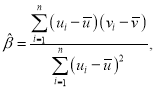题目内容
【题目】已知椭圆![]() 的离心率
的离心率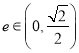 ,
,![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点,![]() ,
,![]() 为椭圆的上、下顶点,且
为椭圆的上、下顶点,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,证明:在第一象限内存在定点
两点,证明:在第一象限内存在定点![]() ,使得当直线
,使得当直线![]() 与直线
与直线![]() 的斜率均存在时,其斜率之和是与
的斜率均存在时,其斜率之和是与![]() 无关的常数,并求出所有满足条件的定点
无关的常数,并求出所有满足条件的定点![]() 的坐标.
的坐标.
【答案】(1)![]() 1;(2)证明见解析,(1,
1;(2)证明见解析,(1,![]() )
)
【解析】
(1)设椭圆的半焦距为![]() ,由
,由![]() ,
,![]() ,
,![]() 的关系和三角形的面积公式,结合离心率公式,解方程可得
的关系和三角形的面积公式,结合离心率公式,解方程可得![]() ,
,![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,联立直线
,联立直线![]() 和椭圆方程,运用韦达定理和判别式大于0,以及斜率公式,化简计算
和椭圆方程,运用韦达定理和判别式大于0,以及斜率公式,化简计算![]() ,考虑它的和为常数,可令
,考虑它的和为常数,可令![]() 的系数为0,进而得到
的系数为0,进而得到![]() 的坐标.
的坐标.
解:(1)设椭圆的半焦距为![]() ,则
,则![]() ,
,
又由![]() 的面积为
的面积为![]() ,可得
,可得![]() ,解得
,解得![]() ,或
,或![]() ,
,
离心率![]() ,则
,则![]() 时,
时,![]() ,舍去,
,舍去,
则![]() ,
,![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() ;
;
(2)证明:设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
将直线![]() 代入椭圆
代入椭圆![]() 可得
可得![]() ,
,
由![]() ,可得
,可得![]() ,则有
,则有![]() ,
,![]() ,
,
 为与
为与![]() 无关的常数,
无关的常数,
可得当![]() ,
,![]() 时,斜率的和恒为0,解得
时,斜率的和恒为0,解得![]() 或
或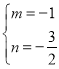 (舍去),
(舍去),
综上所述,在第一象限内满足条件的定点![]() 的坐标为
的坐标为![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.新能源汽车销售的春天来了!从衡阳地区某品牌新能源汽车销售公司了解到,为了帮助品牌迅速占领市场,他们采取了保证公司正常运营的前提下实行薄利多销的营销策略(即销售单价随日销量![]() (台)变化而有所变化),该公司的日盈利
(台)变化而有所变化),该公司的日盈利![]() (万元),经过一段时间的销售得到
(万元),经过一段时间的销售得到![]() ,
,![]() 的一组统计数据如下表:
的一组统计数据如下表:
日销量 | 1 | 2 | 3 | 4 | 5 |
日盈利 | 6 | 13 | 17 | 20 | 22 |
将上述数据制成散点图如图所示:
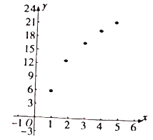
(1)根据散点图判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() ,
,![]() 之间的关系?并从函数增长趋势方面给出简单的理由;
之间的关系?并从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并预测当日销量
的回归方程,并预测当日销量![]() 时,日盈利是多少?
时,日盈利是多少?
参考公式及数据:线性回归方程![]() ,其中
,其中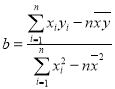 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.