题目内容
【题目】已知点A(﹣1,0),B(1,0)为双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
=1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.x2﹣ ![]() =1
=1
C.x2﹣y2=1
D.x2﹣ ![]() =1
=1
【答案】C
【解析】解:双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0),如图所示,|AB|=|BM|,∠ABM=120°, 过点M作MN⊥x轴,垂足为N,则∠MBN=60°,
=1(a>0,b>0),如图所示,|AB|=|BM|,∠ABM=120°, 过点M作MN⊥x轴,垂足为N,则∠MBN=60°,
在Rt△BMN中,|BM|=|AB|=2a,∠MBN=60°,
即有|BN|=2acos60°=a,|MN|=2asin60°= ![]() a,
a,
故点M的坐标为M(2a, ![]() a),
a),
代入双曲线方程得 ![]() ﹣
﹣ ![]() =1,
=1,
即为a2=b2 ,
由A(﹣1,0),B(1,0)为双曲线的双曲线左右顶点,
则a=b=1,
∴双曲线的标准方程:x2﹣y2=1,
故选:C.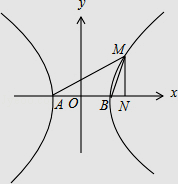

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】某校夏令营有3名男同学![]() 和3名女同学
和3名女同学![]() ,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
一年级 | 二年级 | 三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
(1)用表中字母列举出所有可能的结果;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件![]() 发生的概率.
发生的概率.




