Question

【题目】如图，在四棱锥中，底面为直角梯形，∥，，平面⊥底面，为的中点，，，．

（Ⅰ）求证：平面⊥平面；

（Ⅱ）在棱上是否存在点使得二面角大小为？若存在，求出的长；若不存在，请说明理由.

Answer 1

【答案】(1)证明见解析；(2)答案见解析.

【解析】试题分析：

（Ⅰ）要证面面垂直，就要证线面垂直，题中由已知可得BD⊥AD，再由面面垂直的性质可得BQ⊥平面PAD，从而可得面面垂直；

（Ⅱ）假设存在，以Q为原点建立解析中所示的空间直角坐标系． 写出各点坐标，同时设 ，且，得，求出平面MBQ，平面CBQ的法向量，由法向量的夹角与二面角的关系求出，若求出不出，则说明不存在，求出则说明存在.

试题解析：

(Ⅰ）∵AD // BC，BC=AD，Q为AD的中点，

∴四边形BCDQ为平行四边形，∴CD // BQ ．

∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD．

又∵平面PAD⊥平面ABCD

且平面PAD∩平面ABCD=AD，

∴BQ⊥平面PAD．

∵BQ平面PQB，∴平面PQB⊥平面PAD．

（Ⅱ）假设存在点点使得二面角大小为

∵PA=PD，Q为AD的中点， ∴PQ⊥AD．

∵平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，

∴PQ⊥平面ABCD．

如图，以Q为原点建立空间直角坐标系．

则，，，，

所以 平面BQC的法向量为

由 ，且，得

又，

设平面MBQ法向量

则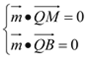

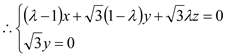
取 ∴ 平面MBQ法向量为．

∵二面角M-BQ-C为30°，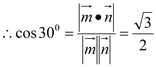

即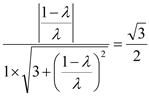 解得 ．

∴

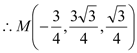所以 存在点M满足时，二面角大小为，

且QM的长度为