题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。曲线
为参数)。曲线![]() 的参数方程为
的参数方程为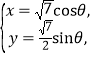 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 的面积(其中
的面积(其中![]() 为坐标原点).
为坐标原点).
【答案】(1) 曲线![]() :
:![]() ,曲线
,曲线![]() :
:![]() .
.
(2)1.
【解析】分析:第一问首先将参数方程消参化为普通方程,之后应用极坐标与平面直角坐标之间的转换关系,求得结果,第二问联立对应曲线的极坐标方程,求得对应点的极坐标,结合极径和极角的意义,结合三角形面积公式求得结果.
详解:(1)由曲线![]() :
:![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() 得:
得:![]()
化简极坐标方程为:![]()
曲线![]() :
: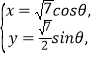 (
(![]() 为参数)消去参数
为参数)消去参数![]() 得:
得:![]()
化简极坐标方程为:![]()
(2)联立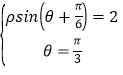
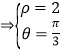 即
即![]()
联立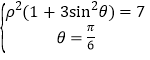
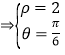 即
即![]()
故![]()

练习册系列答案
相关题目
【题目】某食品企业一个月内被消费者投诉的次数用![]() 表示,据统计,随机变量
表示,据统计,随机变量![]() 的概率分布如列联表.
的概率分布如列联表.
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值和
的值和![]() 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响求该企业在这两个月内共被消费者投诉![]() 次的概率.
次的概率.