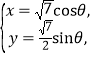题目内容
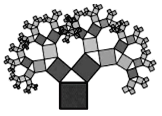
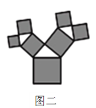
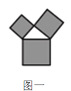
【题目】如图是美丽的“勾股树”，它是一个直角三角形分别以它的每一边向外作正方形而得到.图一是第1代“勾股树”，重复图一的作法，得到图二为第2代“勾股树”，以此类推，已知最大的正方形面积为1，则第n代“勾股树”所有正方形的面积的和为（ ）
A. nB. 
C. 
D. 
【答案】C
【解析】
根据题中所给的条件，最大的正方形的面积为1，从而得到直角三角形的斜边长为1，两个直角边的平方和为1，从而得到图一的三个正方形面积和为2，再算出图二的“勾股树”的所有正方形的面积和为3，观察各选项中的式子求得结果.
最大的正方形的面积为1，
当
时，由勾股定理知正方形面积的和为2，
当
时，从图二中图形的特征，
结合勾股定理以及正方形的面积公式，
求得图二的“勾股树”的所有正方形的面积和为3，
即当时，勾股树的面积为为3，
由此类推，并结合选项，可以得出所有正方形面积的和为
，
故选D.
练习册系列答案
相关题目
