题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的左右顶点分别为
)的左右顶点分别为![]() ,
,![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 不经过点
不经过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过顶点.
过顶点.
【答案】(1) ![]() .
.
(2)见解析.
【解析】分析:第一问利用三角形的面积求得![]() 所满足的关系,结合点在椭圆上,以及椭圆中
所满足的关系,结合点在椭圆上,以及椭圆中![]() 的关系,求得其值,得到椭圆的方程,第二问涉及直线与椭圆相交,需要设出直线的方程,先去验证直线的斜率是存在的,设出方程之后,与椭圆方程联立,消元,利用韦达定理得到其两根和与两根积,利用题中所给的斜率的关系,得出等量关系式,从而求得直线过定点.
的关系,求得其值,得到椭圆的方程,第二问涉及直线与椭圆相交,需要设出直线的方程,先去验证直线的斜率是存在的,设出方程之后,与椭圆方程联立,消元,利用韦达定理得到其两根和与两根积,利用题中所给的斜率的关系,得出等量关系式,从而求得直线过定点.
详解:(1)由题意可设椭圆的半焦距为![]() ,
,
由题意得:
所以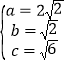
所以椭圆![]() 的方程为:
的方程为:![]()
(2)![]() 当直线
当直线![]() 的斜率不存在时,可设其方程为
的斜率不存在时,可设其方程为![]() 且
且![]() ),
),
不妨设![]() ,
,![]() 且
且![]()
故![]() 把
把![]() 代换化简得:
代换化简得:![]() ,
,![]() 不合题意
不合题意
![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]()
联立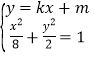
![]()
![]() ,
,
由![]() ,
,![]() 是上方程的两个根可知:
是上方程的两个根可知: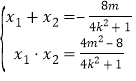
由![]() ,
,![]()
![]()
化简整理得:![]()
即![]()
故![]() 或
或![]() (舍去,因为此时直线经过点
(舍去,因为此时直线经过点![]() )
)
把![]() 代入
代入![]() 得
得![]()
![]()
所以直线方程为![]() (
(![]() ),恒过点
),恒过点![]()

练习册系列答案
相关题目
【题目】某桶装水经营部每天的房租,人员工资等固定成本为200元,每桶水的进价是5元,销售价![]() (元)与日均销售量
(元)与日均销售量![]() (桶)的关系如下表,为了收费方便,经营部将销售价定为整数,并保持经营部每天盈利.
(桶)的关系如下表,为了收费方便,经营部将销售价定为整数,并保持经营部每天盈利.
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | … |
| 480 | 440 | 400 | 360 | 320 | 280 | 240 | … |
(1)写出![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(2)求![]() 表达式,并求其定义域;
表达式,并求其定义域;
(3)求经营部利润表达式![]() ,请问经营部怎样定价才能获得最大利润?
,请问经营部怎样定价才能获得最大利润?