题目内容
在△ABC中,a2+b2-c2=
ab,则角C为( )
| 3 |
| A、60° | B、30° |
| C、120° | D、150° |
考点:余弦定理
专题:解三角形
分析:通过已知条件结合余弦定理,求解即可.
解答:
解:在△ABC中,a2+b2-c2=
ab,
由余弦定理a2+b2-2abcosC=c2,
可得cosC=-
.
解得C=150°.
故选:D.
| 3 |
由余弦定理a2+b2-2abcosC=c2,
可得cosC=-
| ||
| 2 |
解得C=150°.
故选:D.
点评:本题考查余弦定理的应用,三角形的解法,考查计算能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知
=(0,1,1),
=(-2,2,0),则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
在曲线f(x)=x3+3x2+6x-10的切线中,斜率最小的切线方程为( )
| A、x-3y+6=0 |
| B、x+3y-11=0 |
| C、3x+y+11=0 |
| D、3x-y-12=0 |
 △ABC是正三角形,线段EA和DC都垂直与平面ABC,设EA=AB=2α,DC=a,且F为BE的中点,如图:
△ABC是正三角形,线段EA和DC都垂直与平面ABC,设EA=AB=2α,DC=a,且F为BE的中点,如图: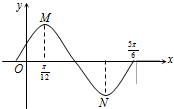 如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<
如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<