题目内容
(本小题满分12分)(注意:在试题卷上作答无效)
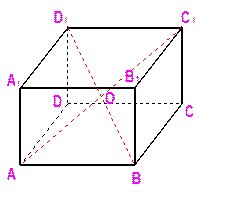
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,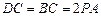 ,
,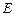 为DB的中点,
为DB的中点,
(Ⅰ)证明:AE⊥BC;
(Ⅱ)线段BC上是否存在一点F使得PF与面DBC所成的角为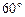 ,若存在,试确定点F的位置,若不存在,说明理由.
,若存在,试确定点F的位置,若不存在,说明理由.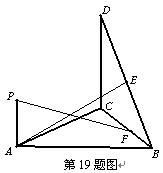
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,
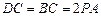 ,
,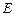 为DB的中点,
为DB的中点,(Ⅰ)证明:AE⊥BC;
(Ⅱ)线段BC上是否存在一点F使得PF与面DBC所成的角为
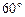 ,若存在,试确定点F的位置,若不存在,说明理由.
,若存在,试确定点F的位置,若不存在,说明理由.
(Ⅰ)证明见解析
(Ⅱ)F为BC的中点
(Ⅱ)F为BC的中点
证明:(I)取BC的中点O,连接EO,AO,
EO//DC所以EO⊥BC ………………………………………………………………….…1分
因为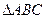 为等边三角形,所以BC⊥AO ……………………………………………3分
为等边三角形,所以BC⊥AO ……………………………………………3分
所以BC⊥面AEO,故BC⊥AE …………………………………………………………4分
(II)方法一:连接PE,因为面BCD⊥面ABC,DC⊥BC
所以DC⊥面ABC,而EO
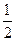 DC
DC
所以EO PA,故四边形APEO为矩形 …………………………………………7分
PA,故四边形APEO为矩形 …………………………………………7分
易证PE⊥面BCD,连接EF,则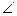 PFE为PF与面DBC所成的角,即
PFE为PF与面DBC所成的角,即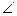 PFE=
PFE=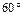 …9分
…9分
在Rt△ PEF中,因为PE =AO=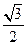 BC,故EF=
BC,故EF=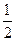 BC,
BC,
因为BC=DC,所以EF=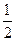 DC,又E为BD的中点,
DC,又E为BD的中点,
所以F为BC的中点……………………………………………………………………..12分
方法二:以BC的中点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,
OE所在的直线为z轴建立空间坐标系,不妨设BC=2,则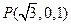 ,设
,设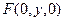 ,
,
则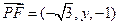 ,………………………………………………………………………7分
,………………………………………………………………………7分
而平面BCD的一个法向量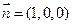 ,则由
,则由
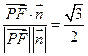 ,………………………………………………………………………..9分
,………………………………………………………………………..9分
解得y=0,故F为BC的中点。……………………………………………………..12
EO//DC所以EO⊥BC ………………………………………………………………….…1分
因为
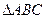 为等边三角形,所以BC⊥AO ……………………………………………3分
为等边三角形,所以BC⊥AO ……………………………………………3分所以BC⊥面AEO,故BC⊥AE …………………………………………………………4分
(II)方法一:连接PE,因为面BCD⊥面ABC,DC⊥BC
所以DC⊥面ABC,而EO

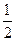 DC
DC所以EO
 PA,故四边形APEO为矩形 …………………………………………7分
PA,故四边形APEO为矩形 …………………………………………7分易证PE⊥面BCD,连接EF,则
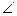 PFE为PF与面DBC所成的角,即
PFE为PF与面DBC所成的角,即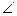 PFE=
PFE=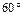 …9分
…9分在Rt△ PEF中,因为PE =AO=
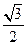 BC,故EF=
BC,故EF=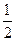 BC,
BC,因为BC=DC,所以EF=
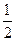 DC,又E为BD的中点,
DC,又E为BD的中点,所以F为BC的中点……………………………………………………………………..12分
方法二:以BC的中点O为原点,OA所在的直线为x轴,OB所在的直线为y轴,
OE所在的直线为z轴建立空间坐标系,不妨设BC=2,则
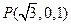 ,设
,设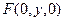 ,
,则
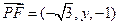 ,………………………………………………………………………7分
,………………………………………………………………………7分而平面BCD的一个法向量
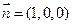 ,则由
,则由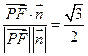 ,………………………………………………………………………..9分
,………………………………………………………………………..9分解得y=0,故F为BC的中点。……………………………………………………..12

练习册系列答案
相关题目
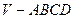 中,底面
中,底面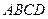 是边长为2的正方形,其余四个侧面都是侧棱长为
是边长为2的正方形,其余四个侧面都是侧棱长为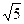 的等腰三角形,且
的等腰三角形,且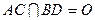 .
.
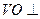 平面
平面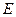 是
是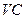 的中点,求
的中点,求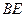 与平面
与平面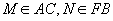 ,且
,且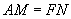 .证明:
.证明: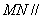 平面BCE.
平面BCE.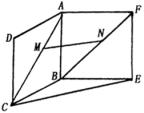
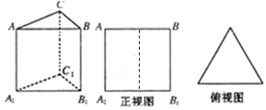
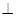 底面A1B1C1,主视图是边长为2的正方形,该三棱柱的左视图面积为
底面A1B1C1,主视图是边长为2的正方形,该三棱柱的左视图面积为 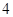
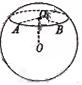
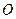 的半径为2,圆
的半径为2,圆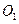 是一小圆,
是一小圆,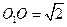 ,
,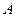 、
、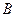 是圆
是圆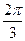 ,则
,则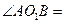 。
。
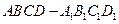 中,
中,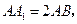
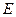 为
为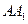 中点,则异面直线
中点,则异面直线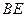 与
与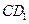 所成的角的余弦值为
所成的角的余弦值为
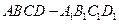 的8个顶点在同一个球面上,且AB=2,AD=
的8个顶点在同一个球面上,且AB=2,AD= ,
, ,则顶点A、B间的球面距离是( )
,则顶点A、B间的球面距离是( )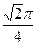 B.
B.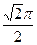 C.
C.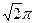 D.2
D.2